这是一篇2016年NIPS的workshop,介绍了变分图自动编码器(VGAE),它是一种基于变分自动编码器(VAE)的无监督学习图结构化数据的框架。 该模型利用了潜在变量,并且能够为无向图学习可解释的潜在表示(请参见图1)。

在Cora引用网络数据集上训练的无监督VGAE模型的潜在空间。
灰线表示引文链接。 颜色表示文档类别(训练期间未提供)。
我们使用图卷积网络(GCN)编码器和一个简单的内积解码器演示了该模型。 我们的模型在引用网络中的链接预测任务上获得了具有竞争力的结果。 与大多数现有的无监督学习图形结构数据和链接预测模型相比,我们的模型可以自然地包含节点特征,从而显着提高了许多基准数据集的预测性能。
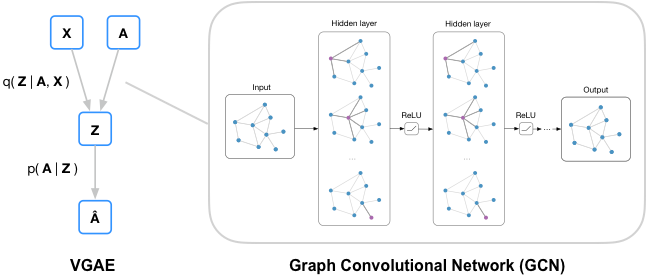
对于上图过程,可以看到变分自编码器学习低维向量表示的分布,包含一个Encoder和一个Decoder, 主要用于推理模型。其中Encoder把input变成概率分布,从概率分布中采样得到隐变量Z,Decoder把这个隐变量Z变成output。
模型
定义
一个无边,无权重的图: $$ G=(V,E)\quad with\quad N=|V|;nodes $$
- 邻接矩阵$A$,对角线元素为1
- 度矩阵$D$
随机潜在向量$z_{i}$,由矩阵$Z(N\times F)$统一,结点特征向量矩阵$X(N\times D)$。
推理模型
通过一个两层GCN进行参数化: $$ q(Z|X,A)=\prod_{i=1}^{N}{q(\vec{z_{i}}|X,A)}\quad with\quad q=(\vec{z_{i}}|X,A)=N(\vec{z_{i}}|\vec{\mu_{i}},\mathrm{diag}(\vec{\sigma_{i}}^{2})) $$ 其中,$\mu=GCN_{\mu}(X,A)$是均值向量$\mu_{i}$的矩阵;$\log{\sigma}=GCN_{\sigma}(X,A)$是方差向量的矩阵;$N(\cdot)$代表服从高斯分布。
两层GCN定义为: $$ \mathrm{GCN}(X,A)=\mathrm{\tilde{A}}\mathrm{ReLU}(\mathrm{\tilde{A}XW_{0}})\mathrm{W_{1}} $$ 其中,$W_{i}$是每一层的权重矩阵,上述两个GCN共享第一层的权重矩阵$W_{0}$。
-
线性整流函数$\mathrm{RuLU}(\cdot)=\max{(0,\cdot)}$
-
对称归一化邻接矩阵$\tilde{A}=D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$
生成模型
通过两个潜在向量之间的内积给出: $$ p(\mathrm{A|Z})=\prod_{i=1}^{N}{\prod_{j=1}^{N}{p(A_{ij}|\vec{z}{i},\vec{z}{j})}}\quad with\quad p(A_{ij=1}|\vec{z}{i},\vec{z}{j})=\sigma(\vec{z}{i}^{T}\vec{z}{j}) $$ 其中$A_{ij}$是矩阵$\mathrm{A}$中的元素,$\sigma(\cdot)$是logistic sigmoid激活函数。
学习
针对变量参数$\bold{W}{i}$优化变量下限$L$: $$ L=E{q(Z|A,X)}[\log{p(A|Z)}]-\mathrm{KL}[q(Z|X,A)||p(Z)] $$ 其中:
-
$E_{q}[\cdot]$是均值;
-
$\mathrm{KL}[q(\cdot)||p(\cdot)]$是$q(\cdot),p(\cdot)$之间的Kullback-Leibler divergence(相对熵)。相对熵可以衡量两个随机分布之间的距离,当两个随机分布相同时,它们的相对熵为零,当两个随机分布的差别增大时,它们的相对熵也会增大。
进一步采用高斯平滑: $$ p(Z)=\prod_{i}{p(z_{i})}=\prod_{i}{N(z_{i}|0,I)} $$ 我们执行批量梯度下降,并利用重新参数化技巧进行训练。 对于无特征的方法,我们只需放弃对X的依赖关系,然后用GCN中的单位矩阵替换X。
非概率图自动编码器(GAE)模型
对于VGAE模型的非概率变体,我们计算嵌入Z和重构的邻接矩阵$\tilde{A}$,如下所示: $$ \tilde{A}=\sigma(ZZ^{T})\quad with\quad Z=\mathrm{GCN(X,A)} $$
代码解读
对于pytorch版本的代码进行一定的解读。
Encoder
# model.py: class VGAE
def encode(self, X):
hidden = self.base_gcn(X)
self.mean = self.gcn_mean(hidden) # 均值GCN
self.logstd = self.gcn_logstddev(hidden) # 方差GCN
gaussian_noise = torch.randn(X.size(0), args.hidden2_dim) # 随机采样
sampled_z = gaussian_noise*torch.exp(self.logstd) + self.mean # 采样还原z'
return sampled_z
Encoder把input变成概率分布,并从概率分布中采样得到隐变量Z。
Decoder
# model.py: class VGAE
def forward(self, X):
Z = self.encode(X)
A_pred = dot_product_decode(Z) # decode
return A_pred
# model.py
def dot_product_decode(Z):
A_pred = torch.sigmoid(torch.matmul(Z,Z.t()))
return A_pred
通过Z和Z转置的点积,可以得到一个对称矩阵,再通过sigmoid函数,可以得到最终的output。
train
for epoch in range(args.num_epoch):
...
loss = log_lik = norm*F.binary_cross_entropy(A_pred.view(-1), adj_label.to_dense().view(-1), weight = weight_tensor)
# 通过交叉熵得到输出矩阵和实际连接矩阵的相似度(结构性)
if args.model == 'VGAE':
kl_divergence = 0.5/ A_pred.size(0) * (1 + 2*model.logstd - model.mean**2 - torch.exp(model.logstd)**2).sum(1).mean()
# 通过相对熵得到理论分布拟合真实分布时产生的信息损耗
loss -= kl_divergence
loss.backward()
optimizer.step()
...
根据公式,L由两部分构成,第一部分为输出矩阵和实际连接矩阵的交叉熵,即两者之间的相似度。连接矩阵反应不同点之间的连接情况,也是一个对称矩阵。第二部分是两个分布之间的相对熵,表示两个分布之间的距离。最终的损失函数为两者之差。