这篇文章提出一种新颖的图形几何交互学习 (GIL) 方法,这是一种非常适合且有效的替代方法,可以利用欧几里得几何和双曲几何的优势,用于学习图形中丰富的几何属性。此外,该方法通过灵活的双特征交互学习和概率组合机制赋予每个节点自由度来确定每种几何空间的重要性。
许多真实的复杂图表现出非欧几何的特征,例如无标度或层次结构。现有双曲空间的工作中,一般假设图中的所有节点共享相同的空间曲率,而不同空间之间没有交互。 与之前方法不同,本文尝试以一种新的交互学习方式将图同时嵌入到欧几里得空间和双曲空间中,希望这两组嵌入可以相互增强,为下游任务提供更有效的表示。GIL 不仅考虑如何交互不同的几何空间,还保证了每个空间的共形不变性。
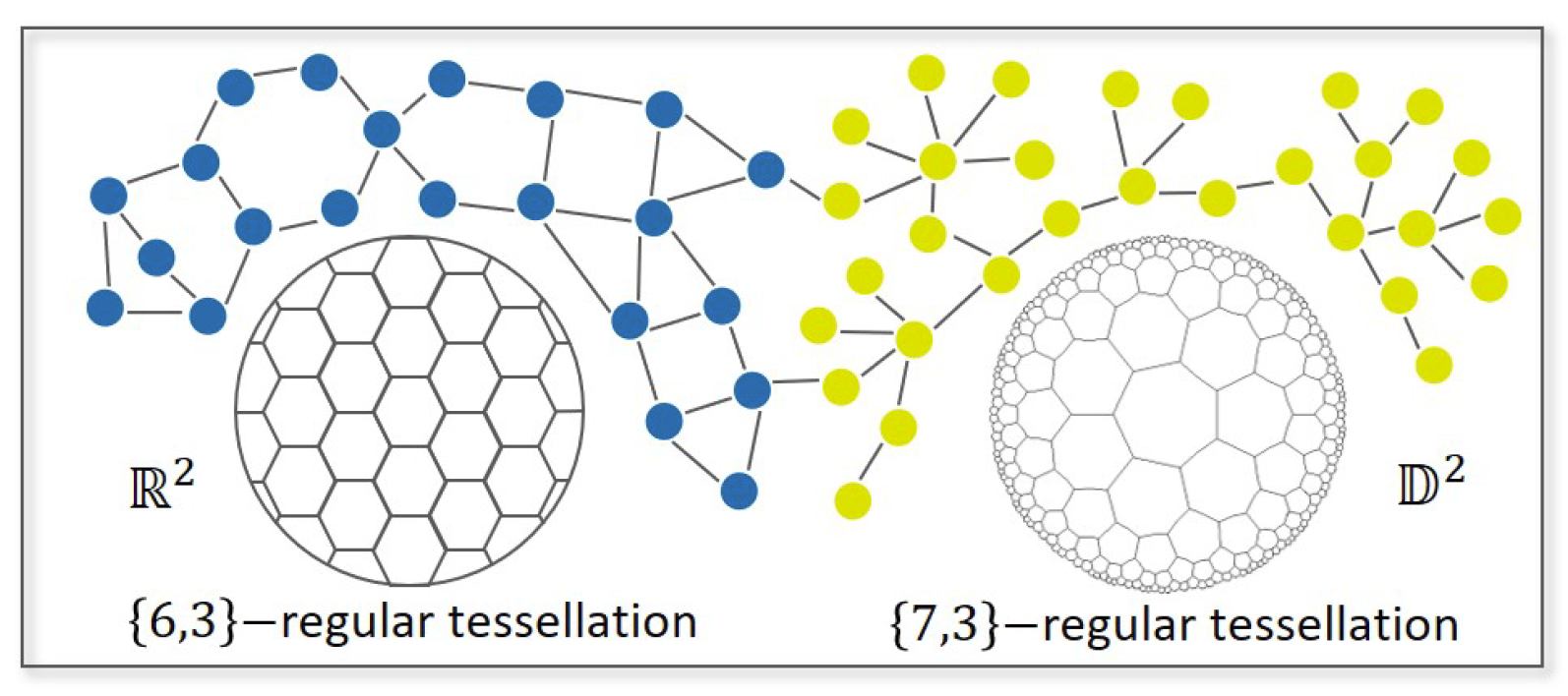
具有双曲线和欧几里德结构的图示
欧几里得空间(左)适合表示低维规则结构的蓝点,而层次结构的黄点更适合表示双曲线空间(右)。
1. 基础定义 Notation and Preliminaries
1.1 双曲几何
该方法在庞加莱模型中进行双曲嵌入,并通过指数变换和对数变换在双曲空间和正切空间之间进行切换。
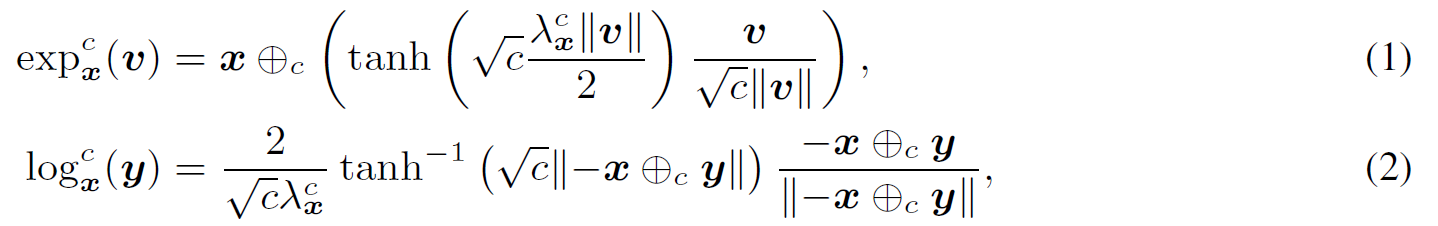
双曲空间中的基本操作为莫比乌斯加法,需要通过定义莫比乌斯加法实现以上操作:
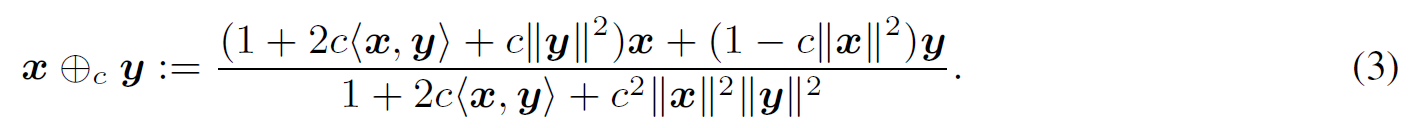
基于莫比乌斯变换,进一步定义在双曲空间中的莫比乌斯标量乘法和莫比乌斯矩阵乘法:
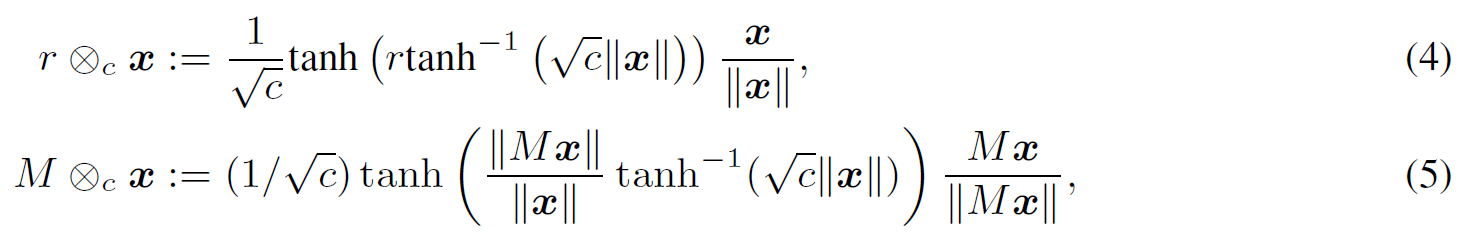
1.2 图注意力网络
图注意力网络(GAT)可以解释为在节点上执行注意力消息传播和更新。每一层通过注意力邻居信息对节点特征$h_{i}$进行更新,得到$h_{i}'$:
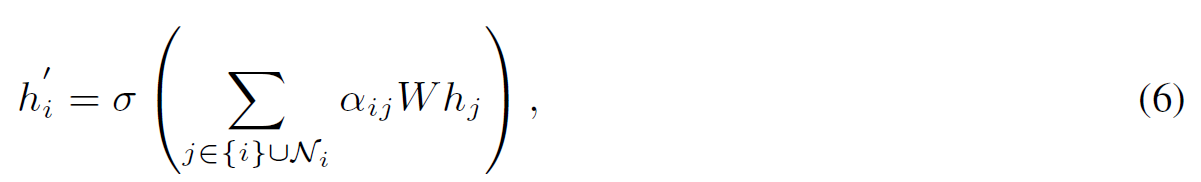
其中$N_{i}$表示节点$i$的单跳邻居,$W$为需要训练的参数。
注意力系数$\alpha_{ij}$通过以下方式计算:
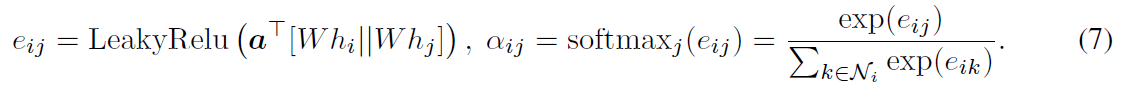
$a$为参数化注意力的权重向量。
2. Graph Geometry Interaction Learning
GIL方法通过特征交互方案利用不同的几何空间,在此基础上进一步开发概率组装以整合最终预测的类别概率。
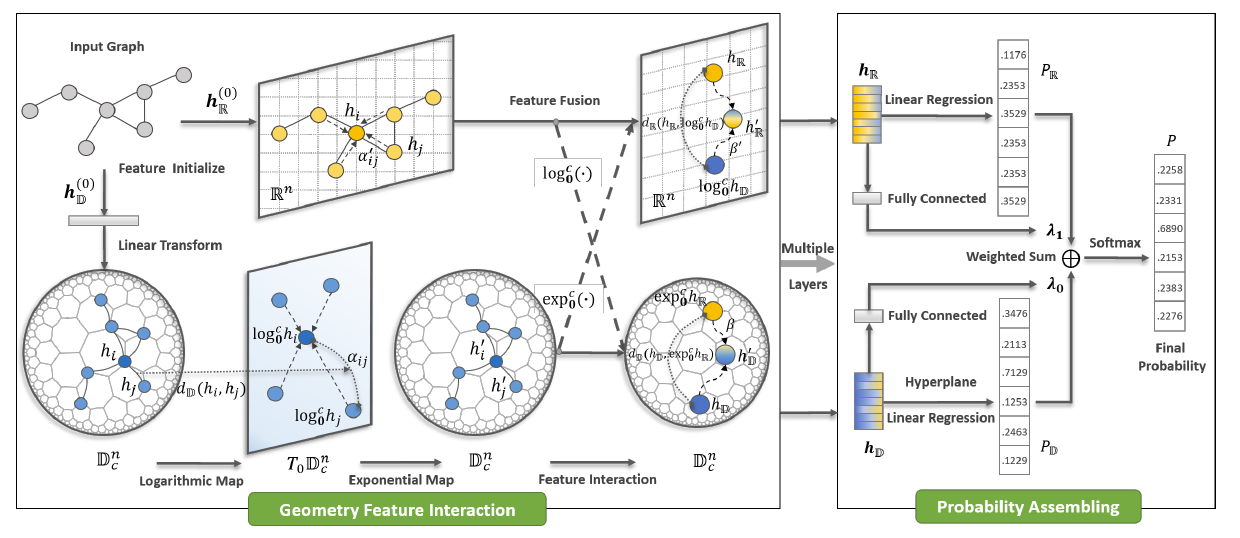
模型GIL分为三个主要部分:
- 几何消息传播(Geometry Message Propagation):通过距离感知注意机制在欧几里得空间和双曲线空间中同时传播邻居信息。 在双曲线空间中,消息通过切线空间上的距离引导的自注意力机制进行聚合;
- 双特征交互(Dual Feature Interaction):节点特征根据距离相似度从双特征空间进行自适应调整;
- 概率组合(Probability Assembling):在训练阶段使用来自每个空间的分类概率的加权和来获得最终的分类结果。
该方法是端到端训练的。
2.1 Geometry Feature Interaction 几何特征交互
2.1.1 几何消息传播
GNN通过消息传播来学习节点嵌入。在欧氏空间中,可以直接使用GAT来进行信息传播。而在双曲空间中,由于莫比乌斯加法不满足交换律和结合律,所以无法直接使用GAT。可以映射到正切空间后,在正切空间中执行以上操作。
对于输入的欧几里得空间的图和节点特征,首先通过指数映射将其映射到双曲空间并进行初始化。初始化得到$h^{(0)}$之后,再通过对数映射到正切空间,进行后续的消息传播。
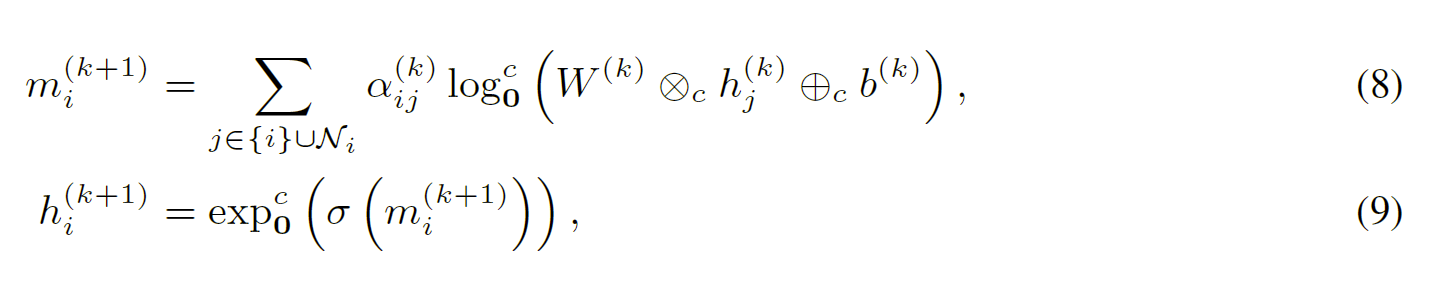
映射到切线空间后,消息通过节点$j$特征的归一化注意力$\alpha_{ij}^{(k)}$缩放到节点$i$(方程10)。 $\alpha_{ij}^{(k)}$是基于距离感知的注意力:
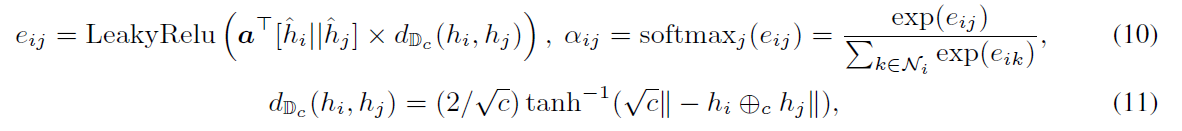
2.1.2 双特征交互
基于图拓扑进行消息传播后,节点嵌入将从双特征空间进行自适应调整,以促进不同几何空间之间的交互。具体来说,通过将双曲嵌入映射到正切空间,欧式嵌入映射到双曲空间来进行交互:
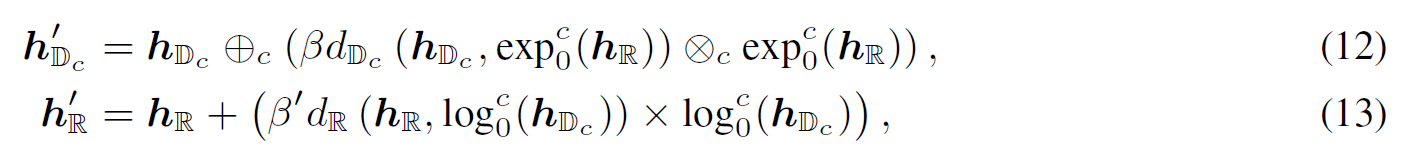
其中,$h'{D{c}}$和$h'_{R}$就是融合之后的节点嵌入。
在特征融合后,因为嵌入仍然回到对应的原始空间中,所以节点嵌入不仅通过交互学习整合了不同的几何特征,而且还保持了原始空间的属性和结构。
2.2 双曲逻辑回归和概率组合
2.2.1 双曲面逻辑回归
为了在双曲空间上执行多类逻辑回归,我们通过引入仿射超平面作为决策边界,将欧几里得 softmax 推广到双曲 softmax。 类别概率通过节点到超平面的距离来衡量:
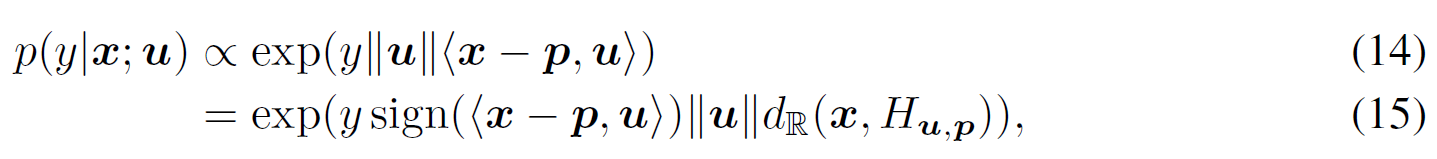
要在双曲空间中定义超平面,需要找出法向量,超平面的方向完全由它决定。由于切线空间是欧几里得空间,因此可以在该空间中直观地定义法向量和内积。

向量$\vec{x}$到超平面$\tilde{H}_{u,p}^{c}$的距离为:
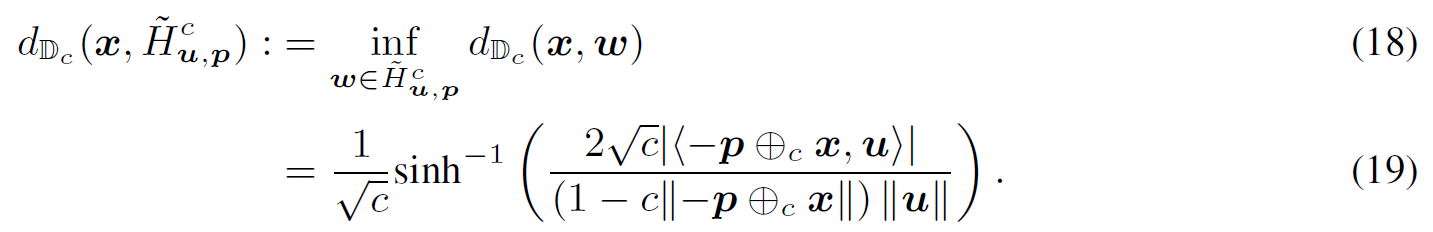
2.2.2 概率组合
最直观和自然的做法是,将不同的几何特征连接起来,然后将单个特征输入一个分类器。 然而,由于几何空间的不同操作,共形不变性的其中之一需要舍弃,要么保留欧几里得方程的空间形式,要么保留双曲线方程的形式:
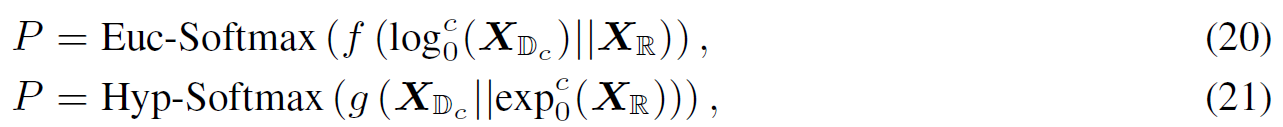
希望同时保持每个空间的特征,并尽可能多地保留空间属性。 所以需要找出对每个节点来说,哪个几何嵌入更重要,然后为相应的概率分配更多权重:
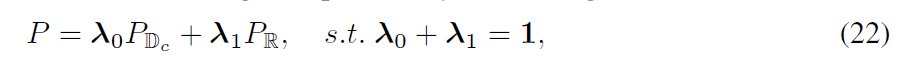
其中对应的权重$\lambda_{0},\lambda_{1}\in R^{N}$表示不同几何概率的节点级权重,通过沿维度1对串联$[\lambda_{0},\lambda_{1}]$进行 L2 归一化来满足归一化条件。分别通过具有相应节点嵌入输入的全连接层进行计算:
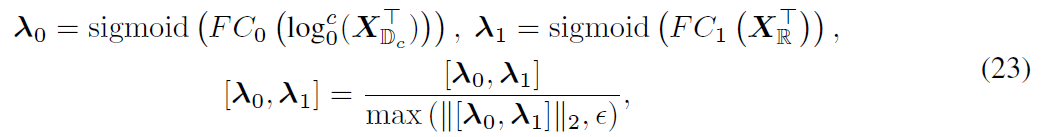
两个空间概率对最终概率的贡献由对应空间中的节点特征决定,即节点本身决定了哪个概率对于下游任务更可靠。
3. 模型总结
本文提出了用于图形的几何交互学习 (GIL),这是一种利用双曲和欧几里得拓扑特征的综合几何表示学习方法。 GIL 为不同的几何结构推导出一种新的距离感知传播和交互学习方案,并以自适应方式为每个节点的不同几何嵌入分配不同的重要性权重。
作者使用端到端架构实现GIL方法,如GIL架构示意图所示。图中左侧面板显示了两个空间之间的消息传播和交互。 对于每一层,局部消息在整个图中扩散,然后节点特征被自适应地合并以根据对偶几何信息进行自我调整。 在堆叠多层使几何特征深度交互后,GIL 应用概率组合得到可靠的最终结果,如图右侧所示。