2021 CVPR Oral A Hyperbolic-to-Hyperbolic Graph Convolutional Network
双曲线图卷积网络 (GCN) 展示了对具有层次结构的图进行建模的强大表示能力。现有的双曲 GCN 求助于切线空间来实现双曲流形上的图卷积,该过程遵循流形-切线-流形方案,如图 1(a) 所示。然而,流形和切线空间之间的映射只是局部微分同胚,这可能会扭曲双曲流形的全局结构,尤其是大量使用切线空间近似之后。
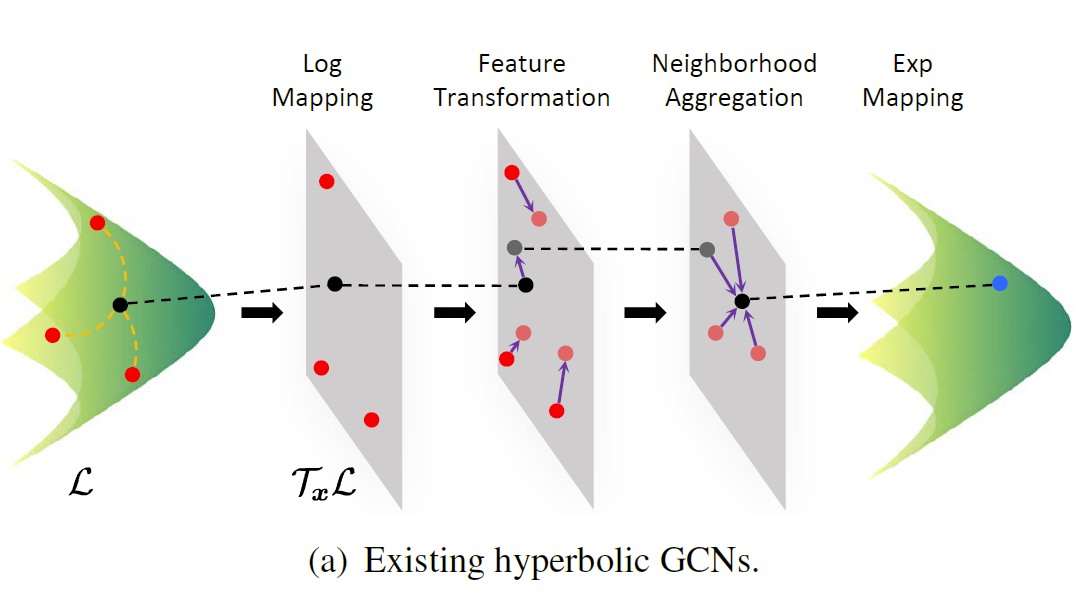
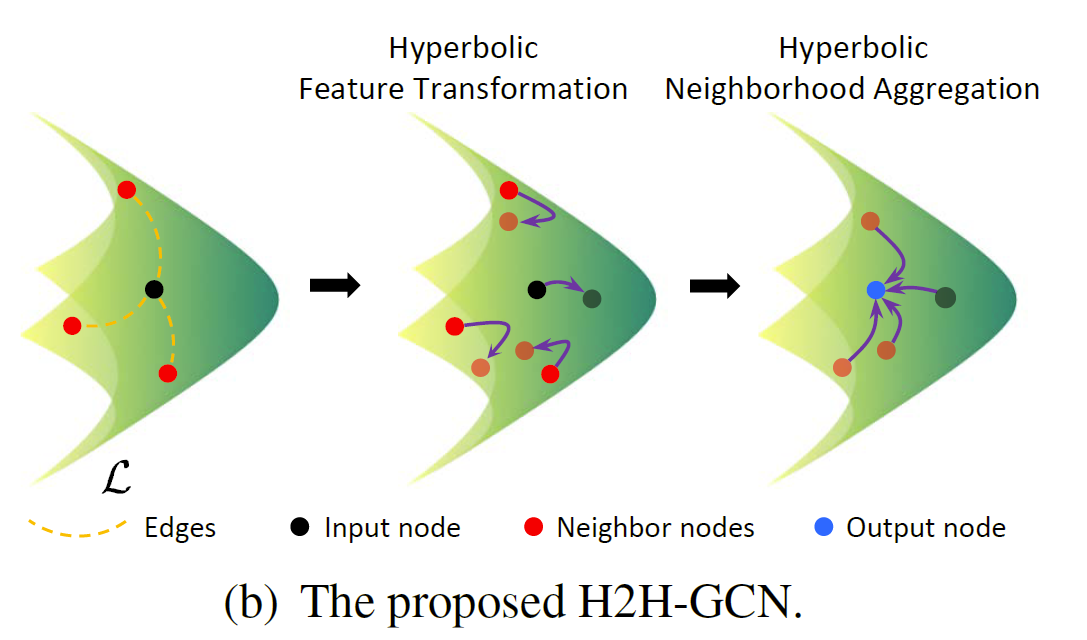
本文提出了一种直接作用于双曲流形的双曲线到双曲线图卷积网络(H2H-GCN),H2H-GCN 避免了由切线空间近似引起的失真并保持全局双曲结构。具体来说,如图1(b)所示,H2H-GCN是一个保留流形的图卷积,它由双曲特征变换和双曲邻域聚合组成。 双曲特征变换作为双曲流形上的线性变换起作用,它通过对变换子矩阵施加正交约束来确保变换后的节点表示仍然位于双曲流形上。 对于双曲线邻域聚合,通过爱因斯坦中点作为邻居节点的加权消息来更新每个节点表示。
1. Preliminaries
1.1 Hyperbolic Spaces
一个$n$维双曲空间的洛伦兹模型定义为$L=\lbrace x=[x_{0},x_{1},…,x_{n}]\in R^{n+1}:<x,x>{L}=-1,x{0}>0\rbrace$,度量张量为$g=\mathrm{diag}([-1,1_{n}^{\top}])$。由$g$诱导的洛伦兹内积为:
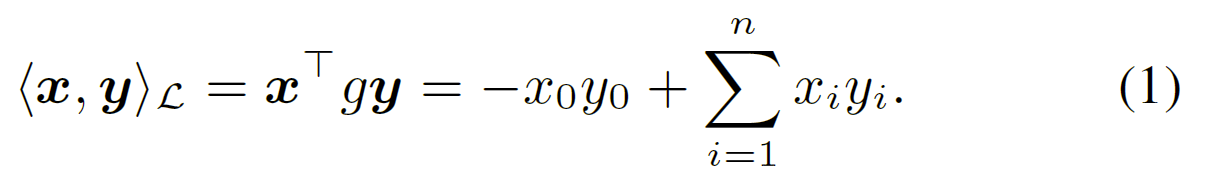
接下来是一些必要操作的定义。
距离 Distance
两个点之间的测地线距离(最短距离):
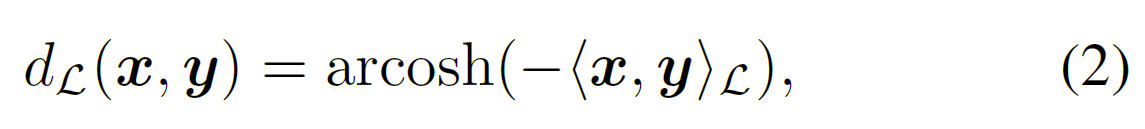
指数、对数映射 Exponential and logarithmic maps
通过指数映射和对数映射实现双曲空间和正切空间之间的切换:
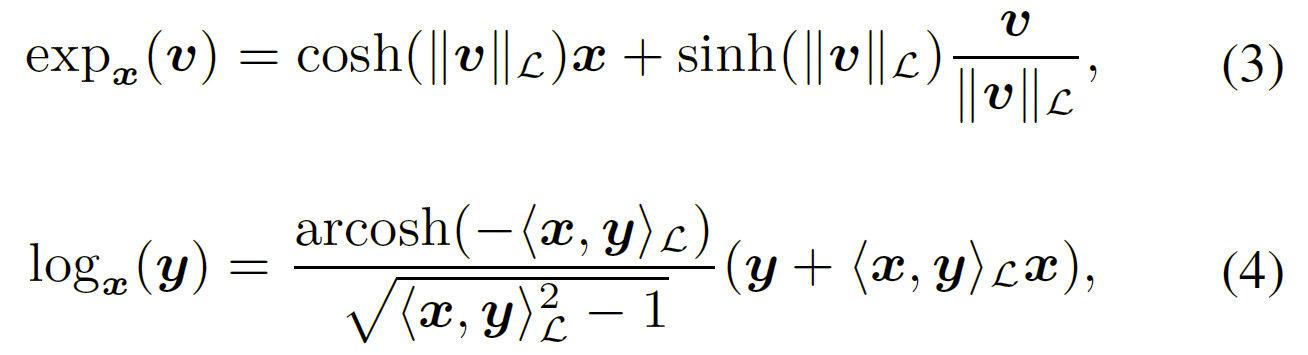
等距同构 Isometric isomorphism
另外两个常见双曲模型为庞加莱模型和克莱因模型。洛伦兹模型和庞加莱模型之间的双射:
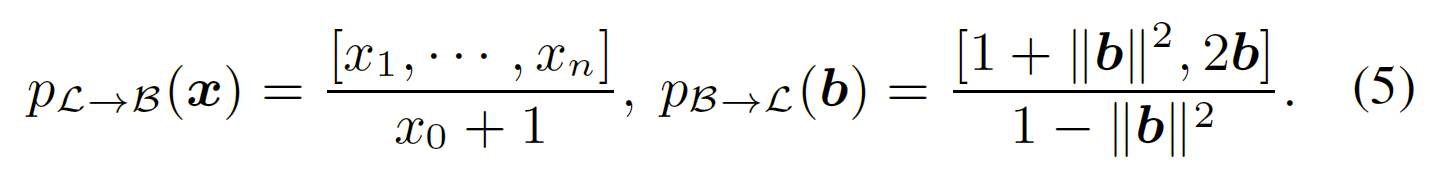
洛伦兹模型和克莱因模型之间的双射:
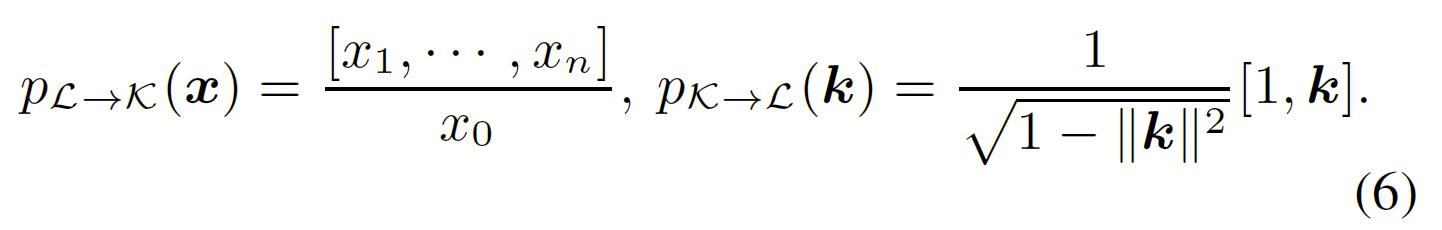
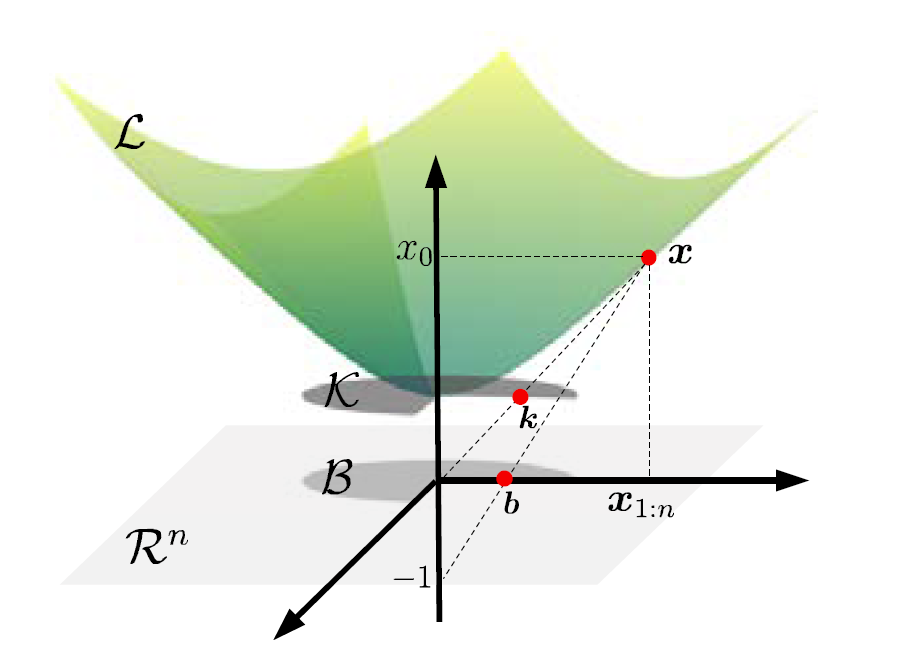
图2给出三种模型之间的几何关系。
1.2 GCNs
在 GCN 的第$l$层,图卷积可以分为两个步骤。
特征变换 Feature Transformation
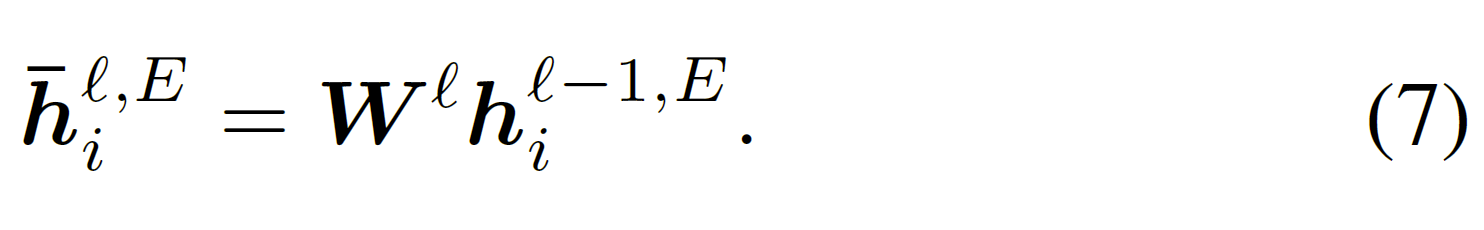
邻域聚合 Neighborhood Aggregation
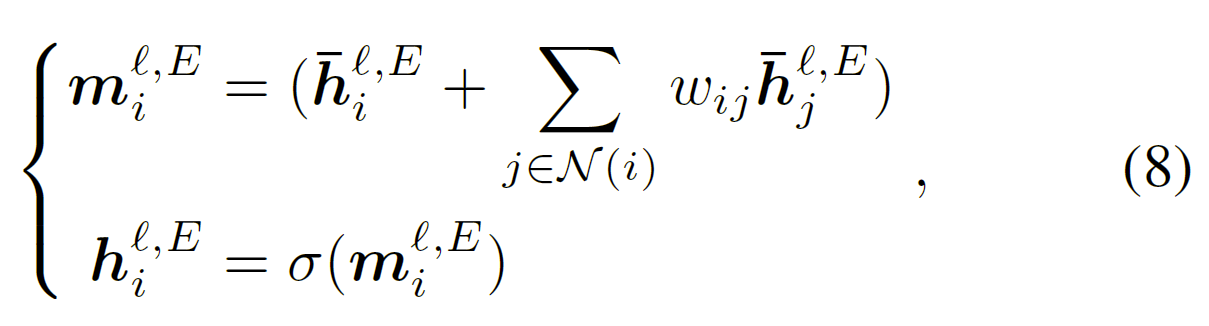
通过堆叠多个图卷积层,特征转换使 GCN 能够为目标任务学习理想的节点嵌入;邻域聚合使 GCN 能够利用图拓扑结构。
2. Hyperbolic-to-Hyperbolic GCN
H2H-GCN 直接对双曲流形进行图卷积以保持全局双曲结构。
2.1 Hyperbolic Node Representations
H2H-GCN 使用方程(3)中定义的指数映射在洛伦兹模型上生成双曲线节点表示:
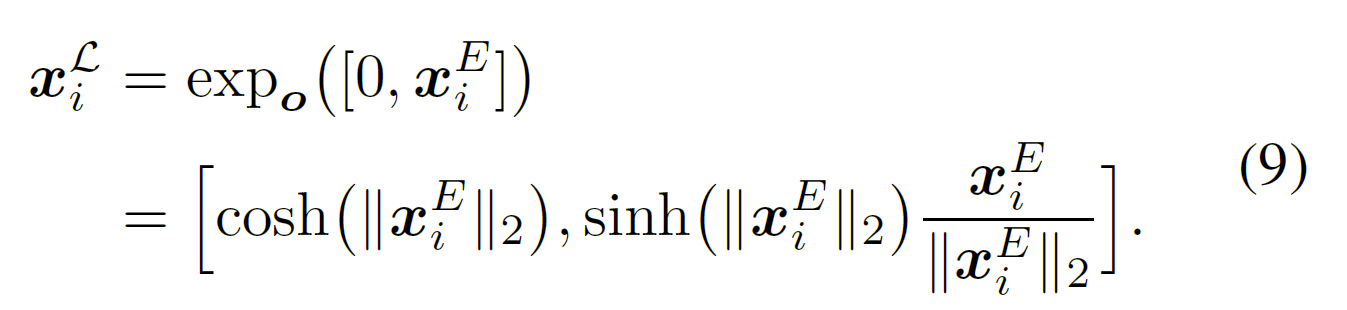
可以合理地认为$[0,x_{i}^{E}]$作为原点 o 处切空间上的节点。
2.2 Hyperbolic Feature Transformation
等式(7)中定义的(欧几里德)GCN 中的特征变换是通过矩阵向量乘法实现的线性变换。尽管如此,在将矩阵向量乘法应用于双曲节点表示时,它将打破双曲流形约束,使变换后的节点不位于双曲流形上,可以通过洛伦兹线性变换来解决这个问题。
定义1. 洛伦兹线性变换
对于$\forall x\in L$,洛伦兹变换定义为:

其中$W$为变换矩阵,$\hat{W}$是变换子矩阵,$0$代表为零的列向量,$I$代表单位矩阵。
利用洛伦兹线性变换作为 H2H-GCN 中的双曲特征变换。在第$l$层,前一层的节点表示$h_{i}^{l-1,L}$和变换矩阵$W^{l}$作为输入。第$i$个节点的中间表示:
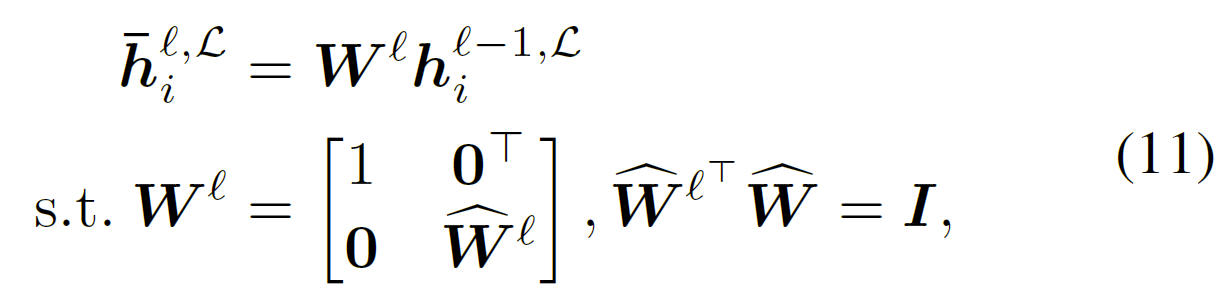
对于第0层,$h_{i}^{0,L}=x_{i}^{L}$.
2.3 Hyperbolic Neighborhood Aggregation
双曲空间中欧几里得均值聚合的推广是 Frechet 均值。 然而,Frechet 均值很难应用,因为它没有封闭形式的解决方案。 所以采用爱因斯坦中点作为 H2H-GCN 中的双曲邻域聚合。在这种情况下,双曲邻域聚合具有两个理想的特性:
- 平移不变性
- 旋转不变性。
聚合双曲线平均对于将输入节点集沿共同方向平移相同距离是不变的,并且对于将输入节点集绕原点旋转相同角度是不变的。
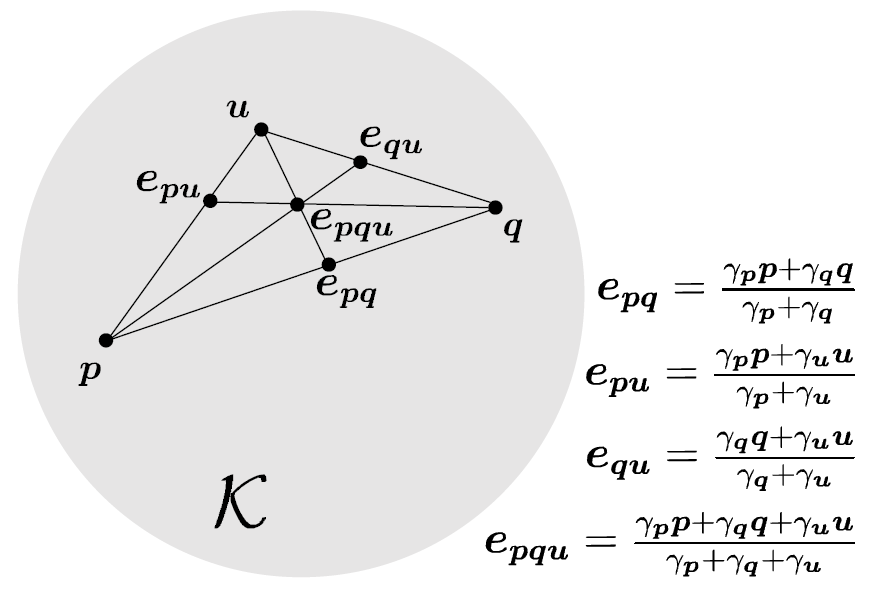
爱因斯坦中点采用克莱因模型中的形式,如图 3 所示。所以,首先需要将洛伦兹模型的中间节点表示投影到克莱因模型,然后通过爱因斯坦中点计算双曲线平均值,最后Klein 模型上的聚合双曲线平均值被投影回 Lorentz 模型。形式上定义为:
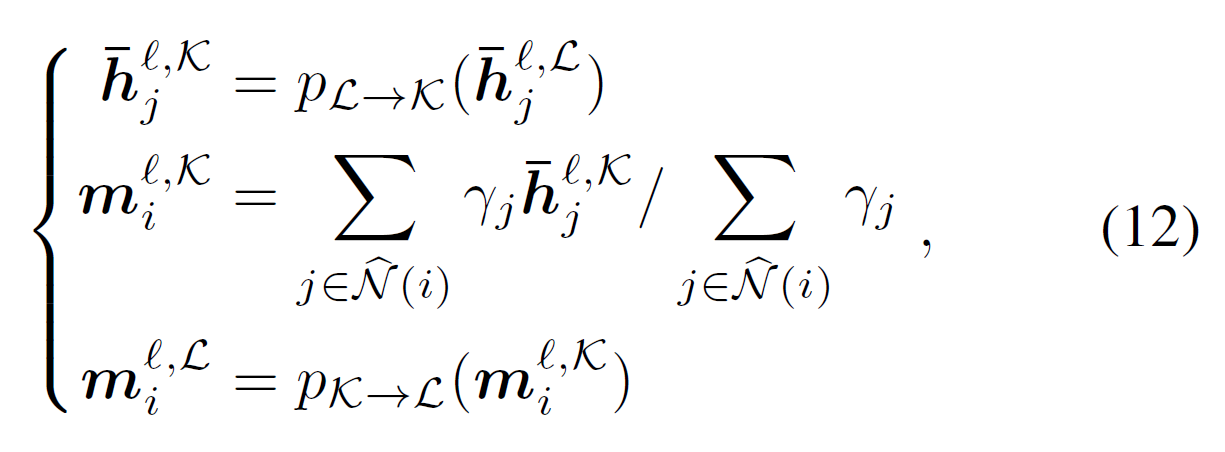
非线性激活在 GCN 中起着重要作用,它可以防止多层网络崩溃成单层网络。然而,在洛伦兹表示上应用常用的非线性激活函数(例如,ReLU)将打破洛伦兹模型的流形约束。 因为 Poincare 球模型上的非线性激活是保持流形的,所以将双曲线平均值$m_{i}^{l,L}$投影到 Poincare 球模型以应用非线性激活,然后将结果投影回洛伦兹模型:
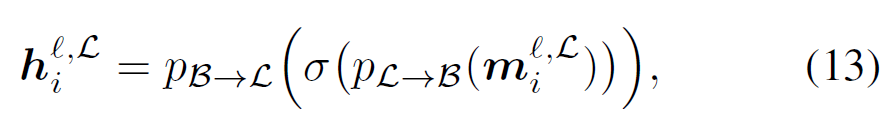
2.4 H2H-GCN Architecture
总结H2H-GCN嵌入生成算法如算法1所示:给定图$G=(V,E)$:
- 将欧几里得特征映射到双曲空间;
- 初始化后的双曲节点特征再通过多层的H2H-GCN;
- 对于第$l$层:
- 对输入的节点特征进行双曲特征变换;
- 进行双曲邻域聚合;
- 通过非线性激活函数。
- 经过$L$层后,得到最终的H2H-GCN节点嵌入。
