该论文推导出一个有理论支撑的半黎曼 GCN,它在图神经网络的上下文中对恒定非零曲率的半黎曼流形中的数据进行建模。 论文方法提供了足够灵活的几何归纳偏置,可以对混合异构拓扑进行建模,例如具有循环的分层图。
比起黎曼流形,配备不定度量的半黎曼流形构成了更大的几何类别。 恒定非零曲率的半黎曼流形不仅概括了双曲流形和球面流形,而且还包含它们的子流形,从而提供特定于这些几何的归纳偏置。
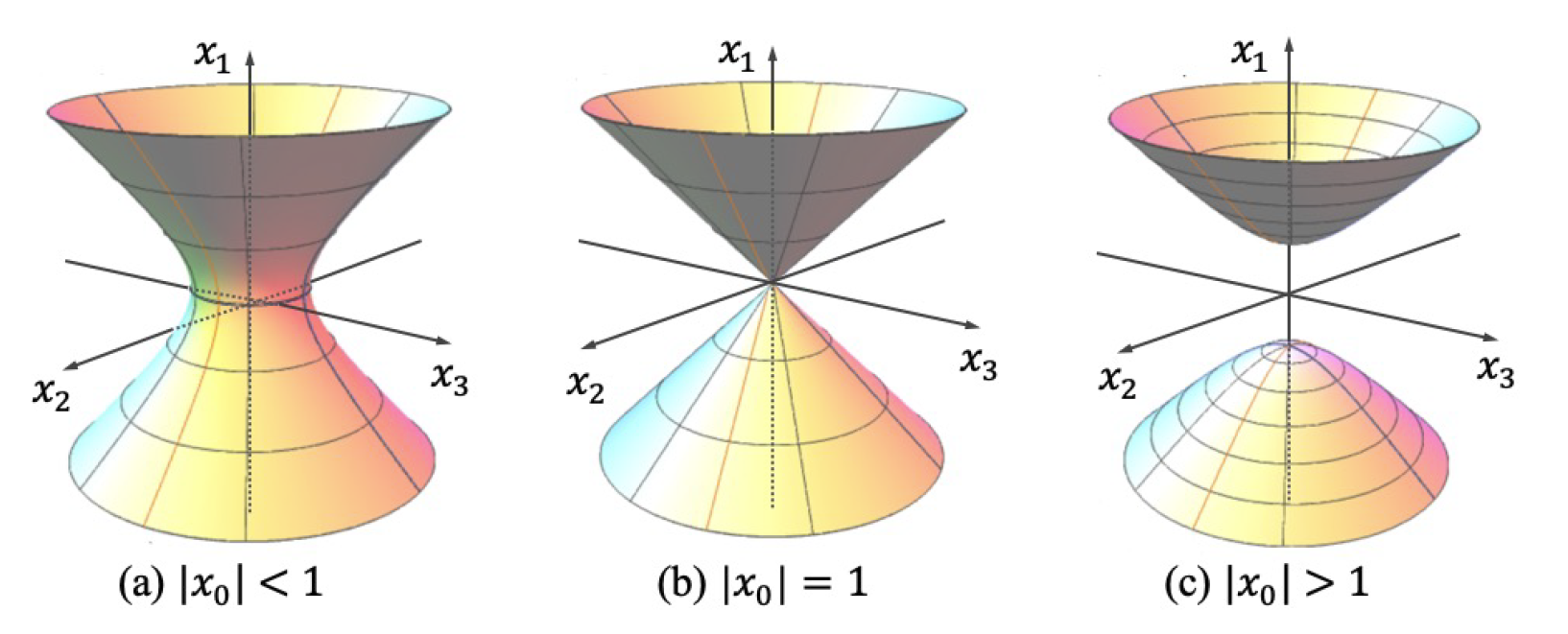
具有两个时间维度的-1曲率四维伪双曲面的不同子流形。 通过固定一个时间维度$x_{0}$,诱导的子流形包括 :(a)一个单层双曲面,(b) 双锥体,和 (c) 一个两层双曲面。
1. 基础定义 Preliminaries
1.1 Semi-Riemannian manifolds 半黎曼流形
半黎曼流形(Semi-Riemannian manifolds),也称为伪黎曼流形(pseudo-Riemannian manifolds)其上有一光滑、对称、点点非退化的$(0,2)$张量。此张量称为伪黎曼度量或伪度量张量。
伪黎曼流形与黎曼流形的区别是它不需要正定(通常要求非退化)。因为每个正定形式都是非退化的,所以黎曼度量也是一个伪黎曼度量,亦即黎曼流形是伪黎曼流形的一种特例。
1.2 Pseudo-hyperboloid 伪双曲面
伪双曲面被定义为周围伪欧几里得空间$R^{s,t+1}$中的子流形,维数为$ d = s + t + 1$,使用方程(1)中的标量积。可以用该标量诱导的范数$||x||^{2}_t=<x,x>t$来定义伪双曲面$Q{\beta}^{s,t}$ :
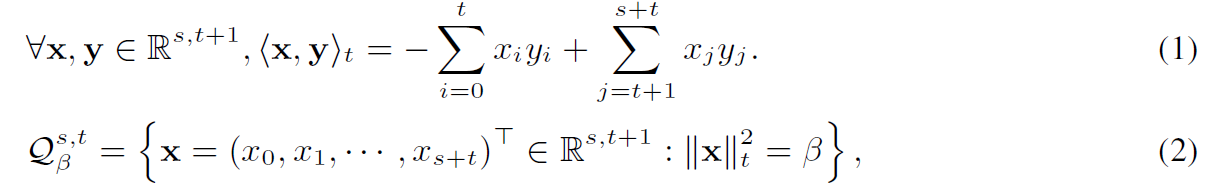
其中,$\beta$是曲率的非零实数参数:
- $\beta>0$:伪球面
- $\beta<0$:伪双曲面
因为$Q_{\beta}^{s,t}$和$Q_{-\beta}^{t+1,s-1}$之间是可互换的,所以只用考虑伪双曲面$Q_{-\beta}^{t+1,s-1}$一种情况即可。根据狭义相对论,$Q_{\beta}^{s,t}$中的一个点$x$可以解释为一个事件,其中最开始的$t+1$维是时间维度,后$s-1$维是空间维度。
双曲流形和球面流形可以分别定义为伪双曲面的特殊情况,方法是将除第1维之外的所有时间维度设置为零得到双曲面流形,将所有空间维度设置为零得到球面流形,即 $$ H_{\beta}=Q_{\beta}^{s,1},S_{-\beta}=Q_{\beta}^{0,t} $$
1.3 Geodesical connectedness 测地连通性
半黎曼流形 M 是连通的,当 M 的任意两点都可以通过分段(断开的)测地线连接,每条测地线都是平滑测地线。 流形是测地连通(g-连通)的,如果任意两点都可以通过测地线平滑连接,其中这两个点称为 g-连通,否则称为 g-断开。
伪双曲面是测地线完备但不是g-连通的流形,其中存在不能通过测地线平滑连接的点。
2. 伪双曲面上的测地线工具 Geodesic Tools on Pseudo-Hyperboloid
2.1 Diffeomorphism of Pseudo-Hyperboloid 伪双曲面的微分同胚
解决微分几何中的难点的一种标准方法是对其更容易操作的微分同胚流形执行操作。
对于半黎曼流形,遵循微分同胚可以将伪双曲面分解为单位球体和欧几里得空间的乘积流形。
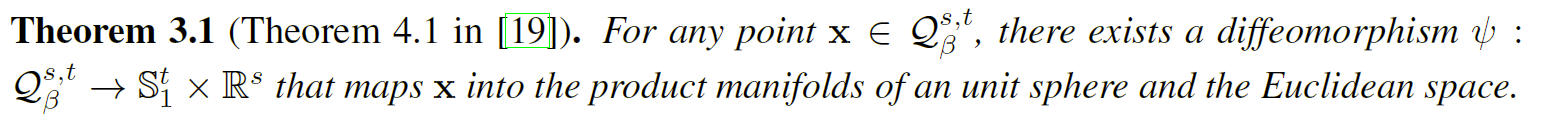
受此启发,我们提出了两个对偶微分同胚,将 x 映射到曲率为$-1/\beta$的球体和欧几里得空间的乘积流形。

定理 3.2 和定理 3.3 分别产生球面投影(用$\psi_{S}$表示)和双曲投影(用$\psi_{H}$表示),并且映射点仍然位于伪双曲面的表面上,如图2(a)。
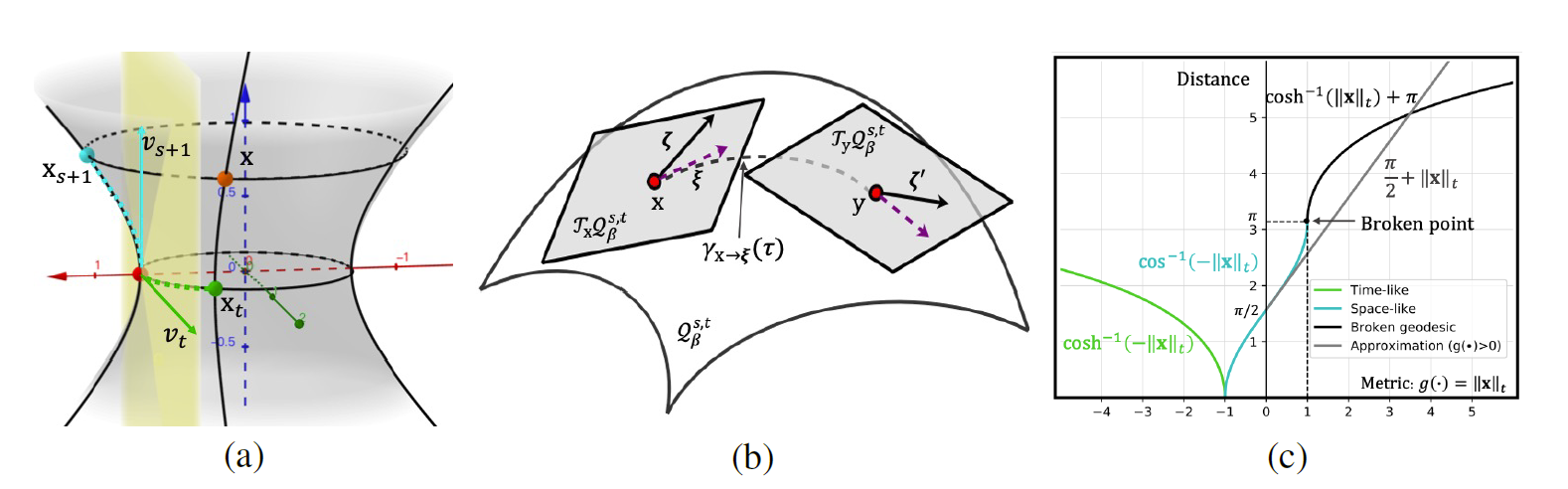
(a) 双曲投影(青色)和球面投影(绿色)分别将点 x(红色)映射到切向量$v_{s+1}$和$v_{t}$;
(b) 平行传输$P_{x\to y}^{\beta}(\xi)$沿正切方向$\xi$将正切向量$\zeta\in T_{x}Q_{\beta}^{s,t}$移动到正切空间$T_{y}Q_{\beta}^{s,t}$;
(c) 分段测地距离(绿色、青色和黑色)和近似部分(灰色)。
事实上,通过推广定理 3.2 和定理 3.3,我们提出了一个更灵活的微分同胚,将伪双曲面分解为乘积流形:
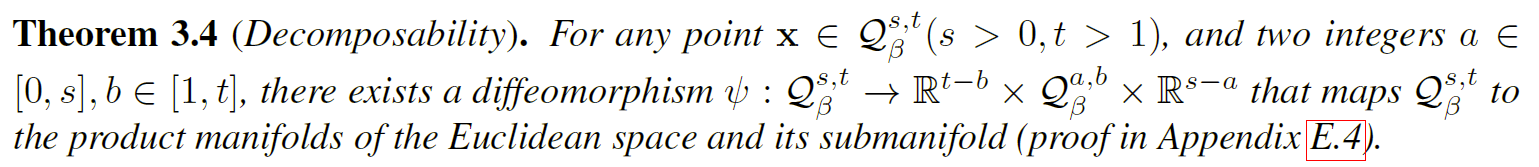
在这种情况下,定理 3.2 和定理 3.3 可以看作是两个特例,分别设置$a=0,b=t$和$a=s,b=1$。当测地线工具在伪双曲面中没有明确定义时,定理 3.4 提供了可分解性作为分析和操作测地线的替代方法。
定理 3.5 表明,并非定理 3.4 中的所有微分流形都是 g-连通的:
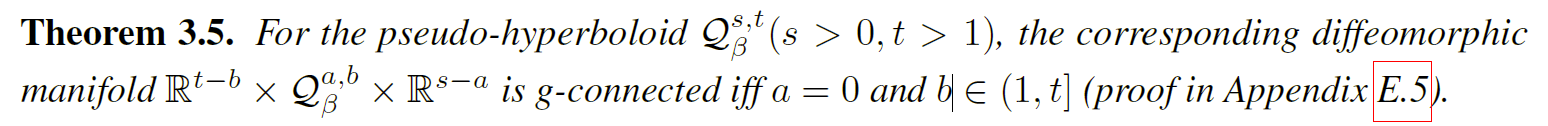
如图1(c)所示,空间维度将导致包含两个孤立的表的双曲子流形,这显然是不连接的。所以,我们必须将所有空间维度都投影到欧几里得空间$R$中。
2.2 Geodesic Tools for G-disconnected Pseudo-hyperboloid 用于G-不连通伪双曲面的测地线工具
Exponential and Logarithmic Map 指数映射和对数映射
如上所述,伪双曲面$Q_{\beta}^{s,t}$是g-不连通的,我们将指数映射和对数映射应用到两个微分同胚流形中:
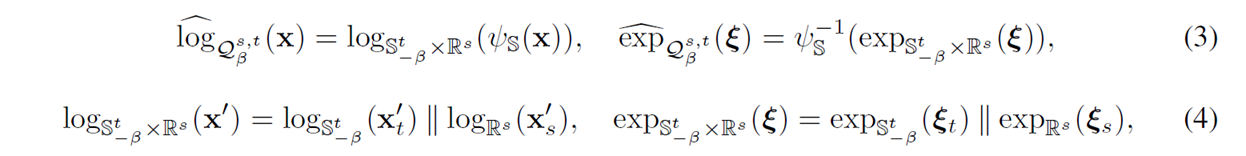
零空间维参考点 x 处的微分同胚映射运算是内在(intrinsic)的,这意味着它们是从伪双曲面上的点到由 x 引起的切线空间的双射函数,由定理 3.6 断言:
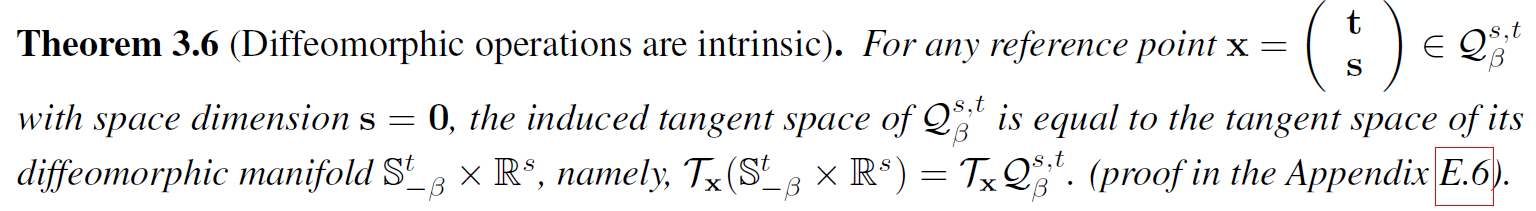
值得注意的是,微分同胚运算的内在性使它们保留了伪双曲面的几何表现力。 这与独立操纵每个组件中的切向量的乘积流形不同。
Tangential Operations 切向操作
通过以上定义的映射操作实现伪双曲面的切向操作:

其中$x$为参考点。
Parallel Transport 平行传输
伪双曲面中的平行传输可以定义为黎曼平行传输的组合。但是,当$ x $和$ y $之间不存在测地线时,无法定义平行传输。 换句话说,$x $引起的切向量不能传递到正交邻域$U_{x}$之外的点的切空间。 直观地,正交邻域满足以下性质:

这可以保证,如果一个点$y\notin U_{x}$,则它的对映点(antipodal point)$-y\in U_{x}$。又因为$T_{y}M$和$T_{-y}M$之间是平行的,所以对于不连通的点,$P_{x\to y}^{\beta}$可以定义为$P_{x\to -y}^{\beta}$。
Geodesic Distance 测地距离
伪双曲面中两个点$x,y$之间的诱导测地距离定义为测地线$\gamma(\tau)$的弧长$d_{\gamma}=\sqrt{||\log_{x}(y)||{t}^{2}}$;对于$\log{x}(y)$无法定义的情况,可以使用近似。如下:
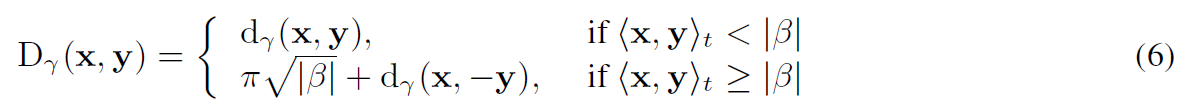
3. 半黎曼GCN Semi-Riemannian GCNs
GCN 可以解释为在对每一层的节点特征进行线性变换后执行邻域聚合。我们通过在伪双曲面$Q_{\beta}^{(s,t)}$中使用开发的测地线工具导出相应的操作来呈现半黎曼 GCN(Q-GCN)。
3.1 Feature Initialization 特征初始化
首先,将欧氏空间中的特征映射到伪双曲面中。然后,我们通过执行由定理3.2或3.3组成的可微映射$\varphi:R_{*}^{t+1}\times R^{s}\to Q_{\beta}^{s,t}$来初始化节点特征。
3.2 Tangential Transformation 正切变换
我们通过利用等式(3)中定义的指数映射和对数映射对切线空间执行欧几里德变换。具体来说,首先通过对数映射将隐藏特征映射到正切空间,然后执行欧几里得矩阵乘法,最后通过指数映射回到原来的流形中。
每一层都执行以上过程,可定义为:
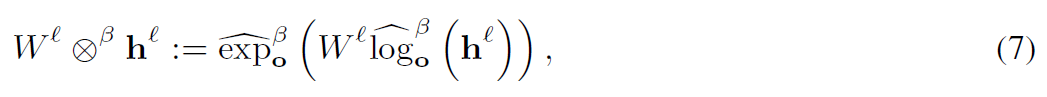
3.3 Bias Translation 偏置平移
为了避免模型崩溃,我们在正切变换后执行偏置平移。通过伪双曲面并行传输,可以通过将切向量平行传输到感兴趣点的切线空间来执行偏置平移。最后再通过指数映射回到原始流形。偏置平移操作可定义为:
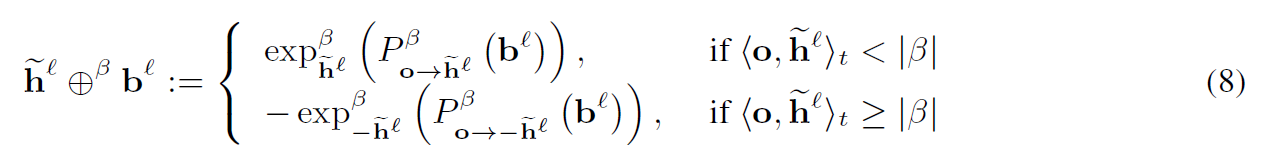
3.4 Tangential Aggregation 正切聚合
邻域特征的线性组合被提升到切线空间,这是微分流形中的一个内在操作。具体来说,Q-GCN在参考点$o$的正切空间中聚合领域嵌入,再通过一个正切激活函数,最后将更新后的表示投影回流形。
在每一层$l$,每个节点$i$的更新特征定义为:
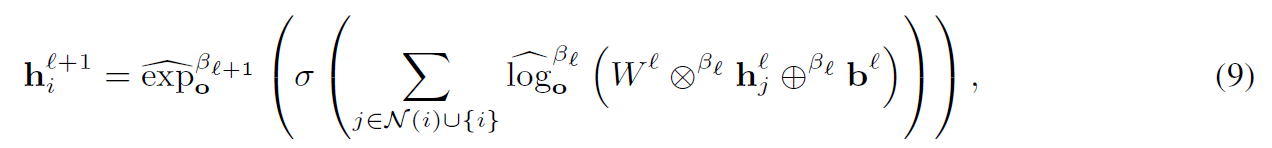
将双曲空间中的逐层可训练曲率推广到伪双曲面,以捕获每层嵌入的正确比例。 最后一层的伪双曲面嵌入可用于下游任务,例如预测节点属性或链接。