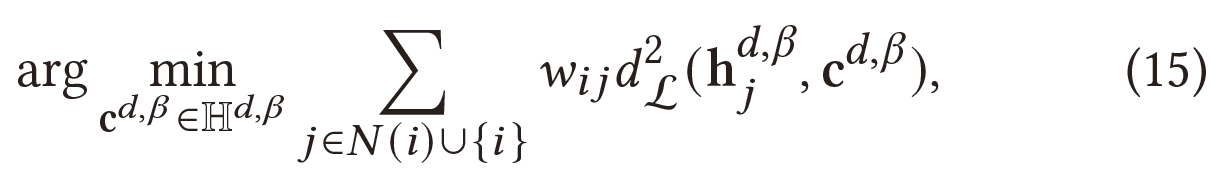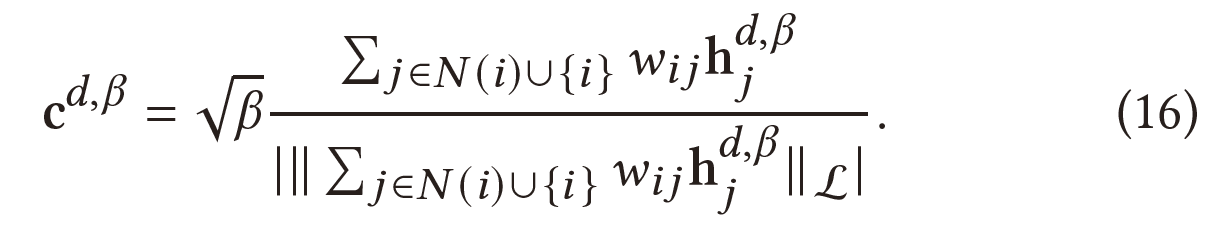大多数 GCN 学习欧几里德几何中的节点表示,但在嵌入具有无标度或分层结构的图的情况下,这可能会产生很大的失真。最近,提出了一些 GCN 来处理非欧几何中的这个问题,例如双曲几何。 尽管双曲 GCN 取得了不错的性能,但现有的双曲图操作(指数、对数映射)实际上不能严格遵循双曲几何,这可能会限制双曲几何的能力,从而损害双曲 GCN 的性能。
为解决以上问题,本文提出一种名为洛伦兹图卷积网络 (LGCN) 的新型双曲 GCN,它在双曲空间的双曲面模型上设计了统一的图操作框架,严格保证学习到的节点特征遵循双曲几何。具体来说,使用洛伦兹重建双曲 GCN 的图操作,例如特征转换和非线性激活。 此外,基于洛伦兹距离的质心设计了一种优雅的邻域聚合方法。 本文提出的图操作在不同类型的双曲几何中是等效的,这也从根本上表明了它们的正确性。
1. Preliminaries
1.1 Hyperbolic geometry
双曲几何是具有恒定负曲率的非欧几何。 双曲面(洛伦兹)模型作为一种典型的能很好地描述双曲几何的等效模型,被广泛使用。洛伦兹标量积定义为:
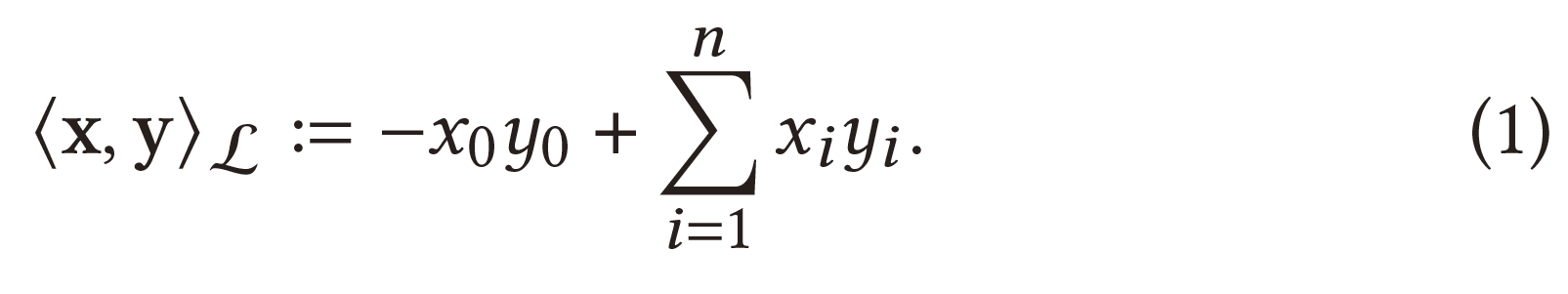
$n$维双曲面流形的定义为:
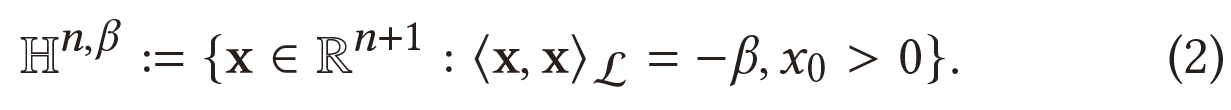
洛伦兹标量积满足:
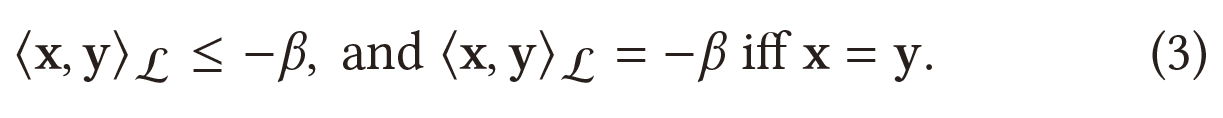
$x$处的切线空间定义为一个$n$维向量空间,近似于$x$周围的$H^{n,\beta}$:
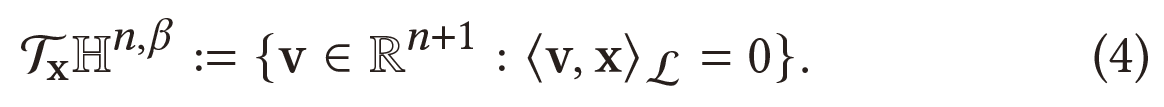
方程(4)具有 Lorentzian 标量积的约束。 切线空间的黎曼度量张量定义为:$g_{x}^{\beta}(v,w):=<v,w>_{L}$。
双曲空间和切线空间之间的映射可以通过指数映射和对数映射来完成:
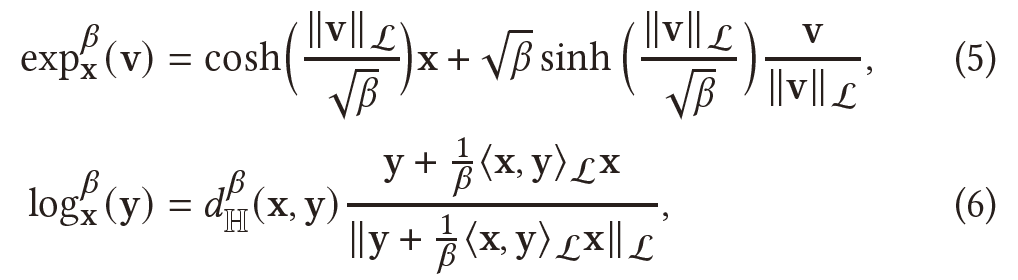
其中两点间的内在距离函数定义为:
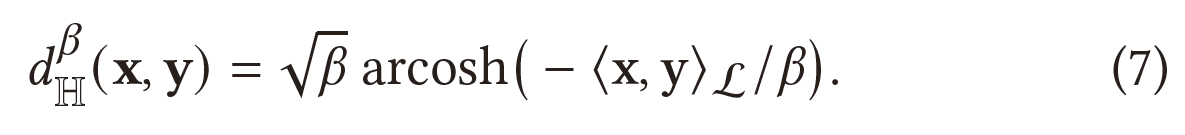
1.2 Hyperbolic graph convolutional networks
本文使用HGCN,将欧几里得图卷积扩展到双曲面模型,作为典型例子来说明双曲GCN的基本框架。HGCN 的消息传递规则包含特征变换:
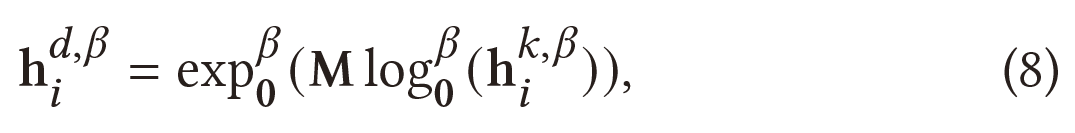
和邻域聚合:
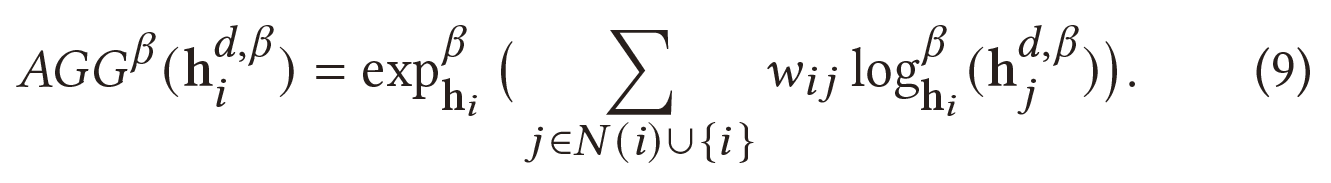
正如方程(8)所示,特征通过对数映射从双曲空间转换到切线空间。然而,因为$<M\log_{0}^{\beta}(h_{i}^{k,\beta}),0>{L}\ne0,0=(\sqrt{\beta},0,…,0)\in H^{k,\beta}$,所以无法满足方程(4)中切线空间$<v,x>{L}=0$的基本约束。因此,通过指数映射将节点特征投影回双曲面流形后,节点特征将超出双曲空间,这不严格满足双曲几何。
回到欧几里得空间,其中进行的节点特征聚合有如下数学意义:
Remark 3.1
给定一个节点,邻域聚合本质上是其局部邻域特征的加权算术平均值。 此外,聚合的特征是几何中邻域特征的质心。
因此,方程(9)中的邻域聚合也应与双曲空间中的欧几里得聚合具有相同的含义。 但是HGCN 中的方程(9) 仅在切线空间而不是双曲空间中满足这些含义,这可能会导致特征失真。 综上所述,上述问题表明现有的双曲线图操作根本不遵循数学,这可能会导致潜在的不可信问题。
2. LGCN
为了解决现有双曲 GCN 的问题,本文提出了 LGCN,它设计了图操作来保证双曲空间中的数学意义。 具体来说,LGCN 首先将输入节点特征映射到双曲线空间,然后通过精心设计的洛伦兹矩阵向量乘法进行特征变换。 此外,提出了基于质心的洛伦兹聚合来聚合特征,聚合权重通过自注意力机制学习。 最后,遵循洛伦兹逐点非线性激活以获得输出节点特征。LGCN中曲率$-\frac{1}{\beta}$同样为可学习的参数。
2.1 Mapping feature with different curvature
LGCN 的输入节点特征可以存在于欧几里得空间或双曲空间中。如果原始特征存在于欧几里得空间中,则需要将它们映射到双曲空间中,此时需要在$h^{k,E}$的第一个坐标处添加一个“0”元素以满足方程(4)约束$<(0,h^{k,E}),0>_{L}=0$,然后再映射到双曲空间:
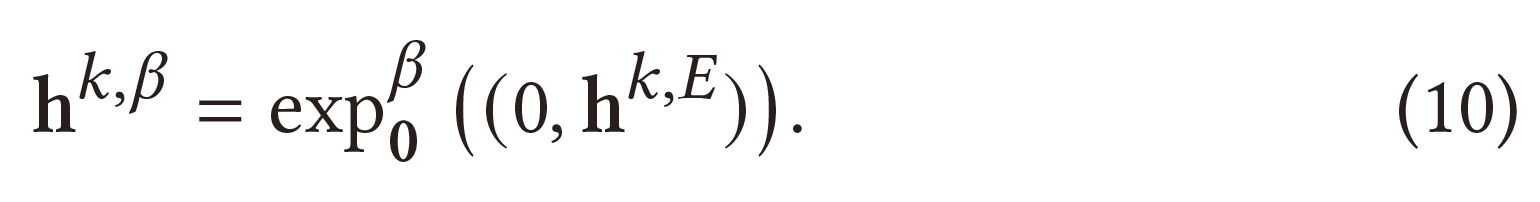
如果输入特征$h^{k,\beta'}$已经在双曲空间中(例如,前一个 LGCN 层的输出),但它的曲率$-\frac{1}{\beta'}$可能与现有流形的曲率并不同,需要将其转化为具有特定曲率$-\frac{1}{\beta}$的双曲面模型:
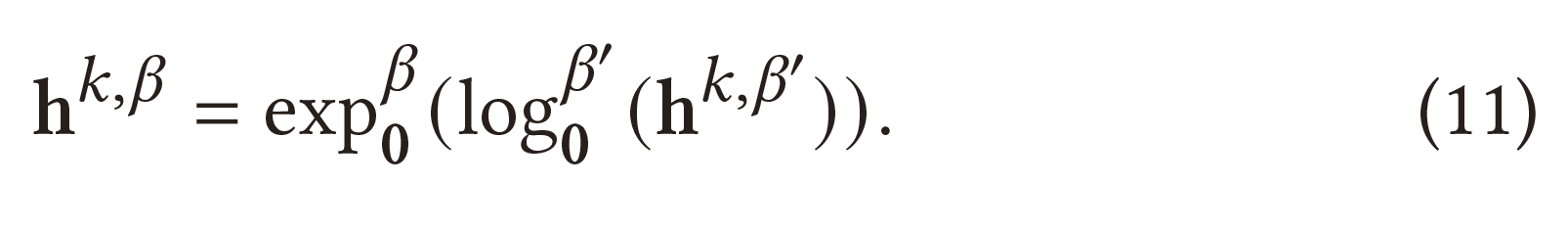
2.2 Lorentzian feature transformation
双曲空间并不是向量空间,这意味着欧几里得空间中的运算不能应用于双曲空间。 为了确保变换后的特征满足双曲几何,在双曲面模型中定义一些规范变换至关重要,因此定义:
Definition 2.1 (Lorentzian version).
不同维度之间的映射:
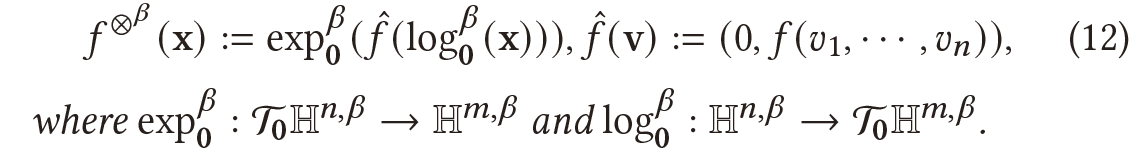
洛伦兹版本利用对数和指数映射来投影双曲空间和切线空间之间的特征。由于切线空间是向量空间并且与$R^{n}$同构,因此欧几里得变换可以应用于切线空间。与之前方法不同的是,洛伦兹版本只利用了切线空间中最后$n$个坐标$(v_{1},…,v_{n})$上的欧几里德变换,并且将第一个坐标$v_{0}$置为“0”以满足方程( 4)中的约束。因此,此操作可以确保变换后的特征严格遵循双曲几何。
为了在双曲面模型上应用线性变换,遵循洛伦兹版本,可以导出洛伦兹矩阵向量乘法:
Definition 2.2 (Lorentzian matrix-vector multiplication).
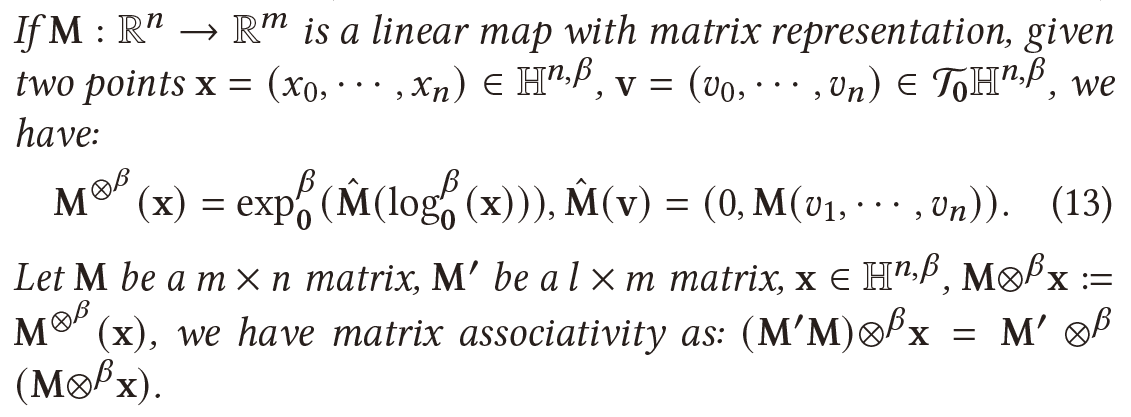
洛伦兹矩阵向量乘法与双曲面模型上的其他矩阵向量乘法之间的一个主要区别是矩阵 M 的大小。假设需要将$ 𝑛 $维特征转换为$m$维特征,矩阵 M 的大小应该是$m\times n$,这是洛伦兹矩阵-向量乘法所满足的。然而,对于其他方法,如方程(8),矩阵M的大小为$(m+1)\times (n+1)$,导致不能满足切线空间的约束$<M\log_{0}^{\beta}(h_{i}^{k,\beta}),0>_{L}\ne0$,所以转换后的特征将超出双曲空间。 此外,洛伦兹矩阵向量乘法具有以下性质:
Theorem 2.1.
给定双曲空间中的一个点,双曲面模型表示为$x^{n,\beta}\in H^{n,\beta}$,庞加莱球模型表示为$x^{n,\alpha}\in D^{n,\alpha}$。令$M$为一个$m\times n$的矩阵,双曲面模型中的洛伦兹矩阵向量乘法$M\otimes^{\beta}x^{n,\beta}$与庞加莱球模型中的莫比乌斯矩阵向量乘法$M\otimes^{\alpha}x^{n,\alpha}$是等价的。
这个属性优雅地桥接了双曲面模型和庞加莱球模型之间矩阵向量乘法的关系。 可以使用洛伦兹矩阵向量乘法对双曲面模型进行特征变换为:

2.3 Lorentzian neighborhood aggregation
与 Remark3.1一样,在欧几里得空间中,邻域聚合是计算其邻域特征的权重算术平均值或质心(也称为质心),如图1(a)所示。
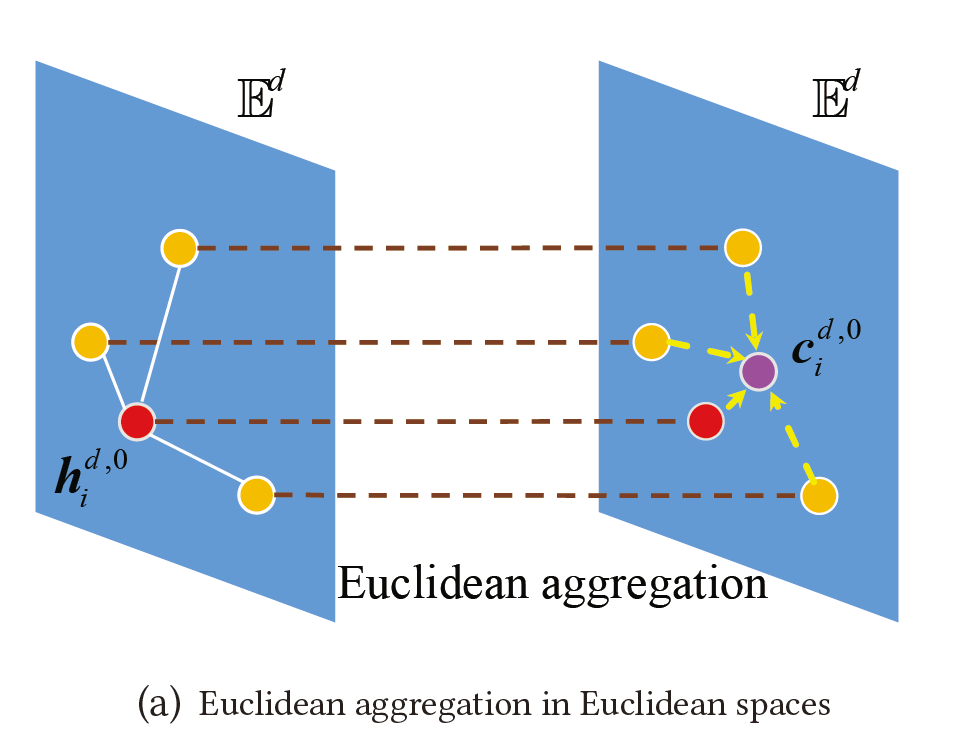
LGCN目标是聚合双曲线空间中的邻域特征并遵循这些含义。 Fréchet 均值提供了一种可行的方法来计算黎曼流形中的质心。 此外,算术平均值也可以解释为一种 Fréchet 平均值。 因此,Fréchet mean 符合邻域聚合的含义。 Fréchet 均值的主要思想是最小化一组点的(平方)距离的期望。 然而,Fréchet mean 没有一个关于双曲空间中的内在距离$d_{H}^{\beta}$的封闭形式的解,它必须通过梯度下降进行低效计算。 因此,本文提出了一种优雅的基于平方洛伦兹距离的质心的邻域聚合方法,可以很好地平衡数学意义和效率:
Theorem 2.2 (Lorentzian aggregation via centroid of squared Lorentzian distance).
对于一个节点特征$h_{i}^{d,\beta}\in H^{d,\beta}$,其一组邻域节点$N(i)$,对应聚合权重为$w_{ij}$,邻域聚合包含在节点的质心$c^{d,\beta}$中,这将问题最小化:
这个问题有封闭形式的解决方案:
其中用到的平方洛伦兹距离公式定义为:
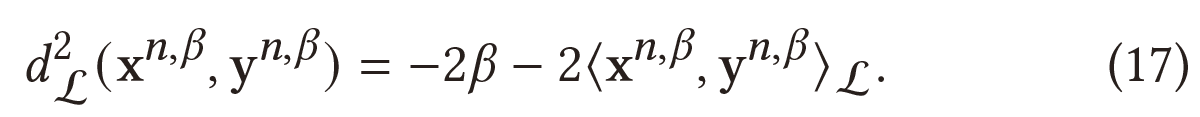
图 1(b) 说明了通过质心的洛伦兹聚合。 类似于 Fréchet/Karcher 均值,由洛伦兹聚合计算的节点特征是平方洛伦兹距离的期望值的最小值。 此外,洛伦兹邻域聚合中的聚合特征是几何中双曲面模型中的质心 。
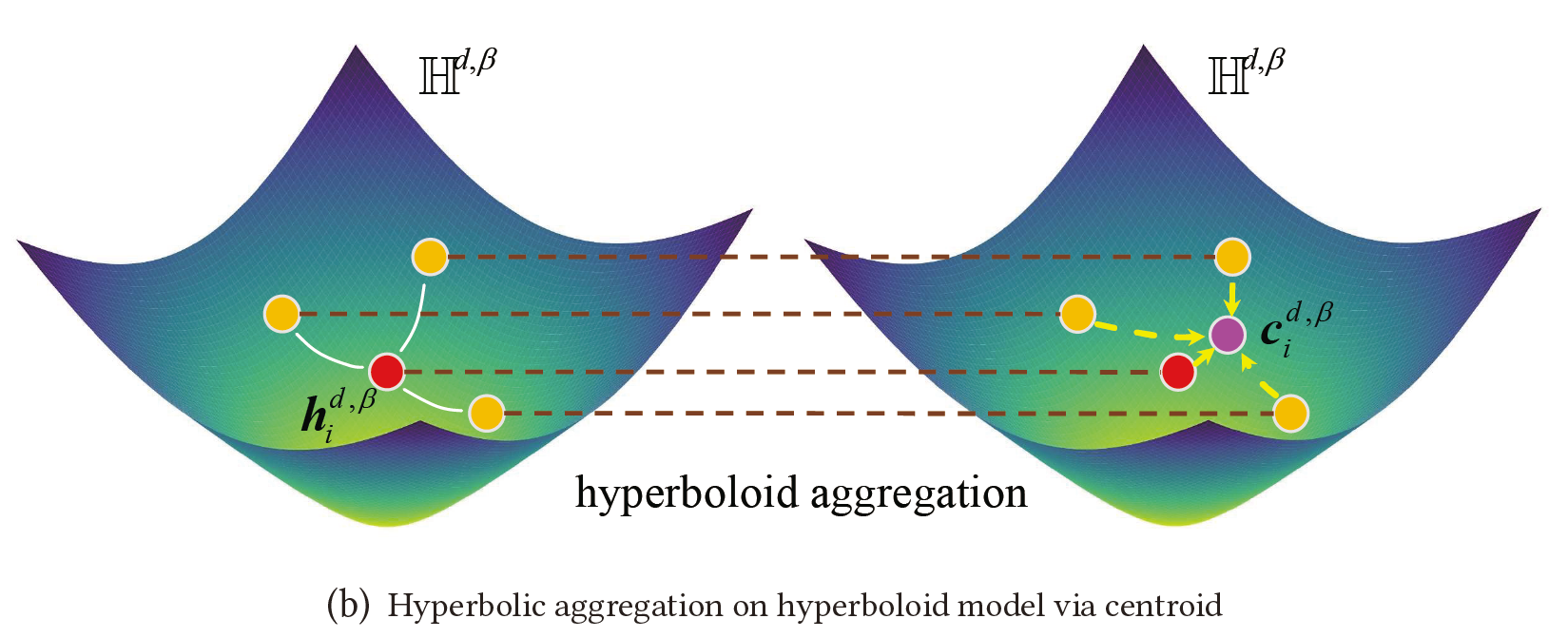
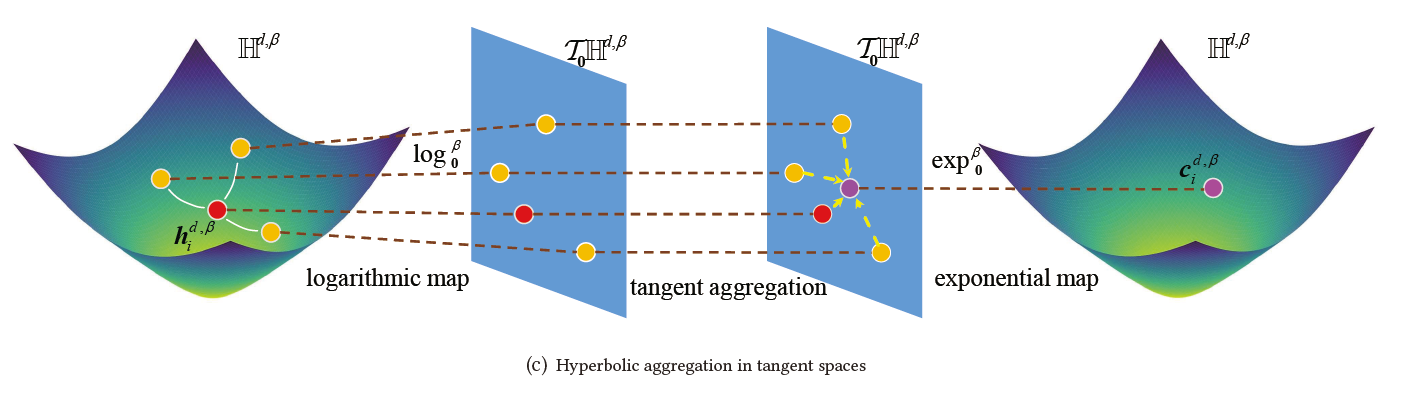
另一方面,一些双曲 GCNs聚合了切线空间中的邻域(如图 1(c) 所示),只能在切线空间中视为质心或算术平均值,而不是在双曲线空间。 因此,通过平方洛伦兹距离的质心进行洛伦兹聚合是一种很有前途的方法,与其他双曲 GCN 相比,它满足更优雅的数学含义。
如方程(16)所示,有一个聚合权重$w_{ij}$表示邻域对于中心节点的重要性。 这里提出了一种自注意力机制来学习聚合权重$w_{ij}$。对于两个节点特征,注意力系数$\mu_{ij}$表示节点$i\to j$的重要程度,计算公式为:
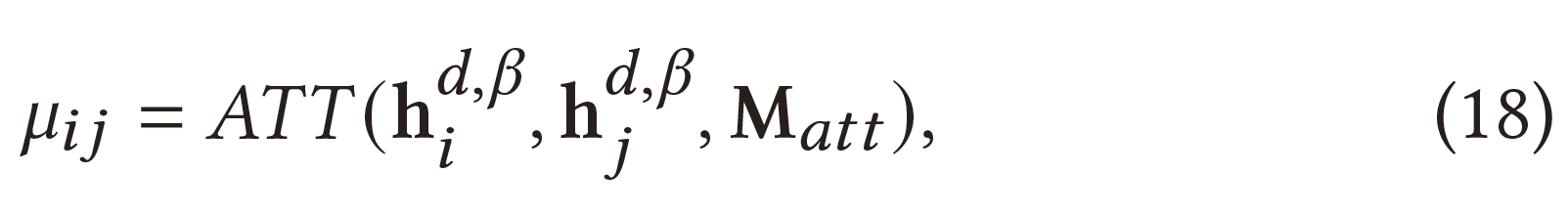
其中𝐴𝑇𝑇(·)表示计算注意力系数的函数,而𝑑×𝑑矩阵$M_{att}$是将节点特征转化为基于注意力的特征。考虑一个较大的注意系数$\mu_{ij}$表示$i,j$节点的高度相似性, 基于洛伦兹距离的平方定义𝐴𝑇𝑇 (·):
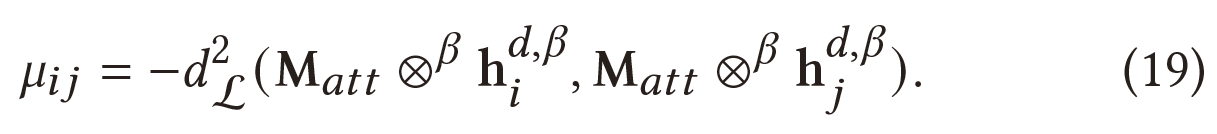
对于所有的邻居𝑁 (𝑖) 节点的𝑖 (包括其本身),使用softmax函数对其进行规范化,以计算聚合权重:
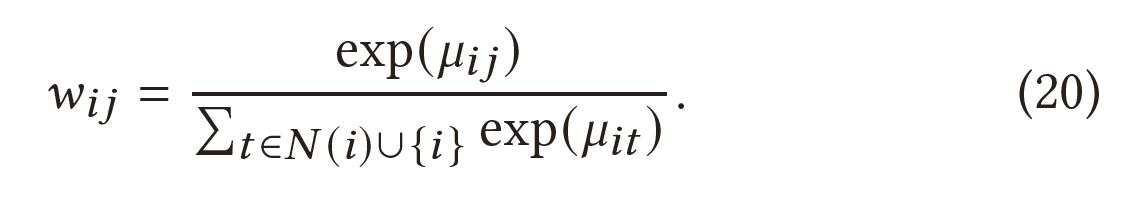
2.4 Lorentzian pointwise non-linear activation
非线性激活是GCN不可缺少的一部分。与特征转换类似,双曲面模型上现有的非线性激活也会使特征脱离双曲面模型。这里根据洛伦兹版本推导出洛伦兹点态非线性激活:
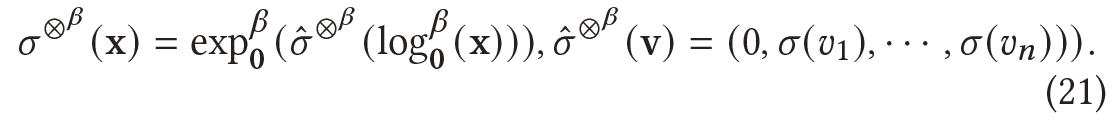
洛伦兹点态非线性激活不仅保证了变换后的特征仍然存在于双曲空间中,而且具有如下性质。
Theorem 4.3.
双曲面模型中的洛伦兹点态非线性$\sigma^{\otimes^{\beta}}(x^{n,\beta})$等价于庞加莱球模型中的莫比乌斯点态非线性$\sigma^{\otimes^{\alpha}}(x^{n,\alpha})$,𝜎(·) 表示某些特定的非线性激活,例如Relu、LEKLYRELU。
这一特性也在两个模型中架起了点态非线性的桥梁。洛伦兹点态非线性激活后,LGCN层的输出为:

这可用于下游任务,如链路预测和节点分类。
3. 总结
这篇文章提出的LGCN模型的思路和之前的HGCN思路大致相同,都是采用双曲-切线-双曲的模式,本文的不同在于改进了双曲-切线之间的映射函数,使其不违背双曲约束,能够保留双曲特征。