STRUC2VEC的目的是捕捉网络中节点的结构信息(潜在表示):
- 结构相似节点的表示应该相似(距离近);结构不同的节点表示应该不同(距离远);
- 节点结构的潜在表示不依赖于节点、边的标签等属性,只与节点在网络中的“位置有关”。
1. 结构相似度 Structural Similarity
直观上,两个度(degree)相同的节点在结构上相似。令$G=(V,E)$表示无向、无权重的网络,其中节点集$V$,节点数量为$n=|V|$,边集$E$,$k^{*}$表示网络的直径。令$R_{k}(u)$表示距离节点$u;k$跳的节点集合。$s(S)$表示集合$S\subset V$的有序度序列。
通过比较距离 $u$ 和$v$为$k$的环的有序度序列,我们可以施加层次结构来测量结构相似性。令$f_{k}(u,v)$表示$u,v$之间的结构距离(structural distance),考虑$k$跳的距离(距离小于或等于$k$的所有节点以及其中的所有边)。
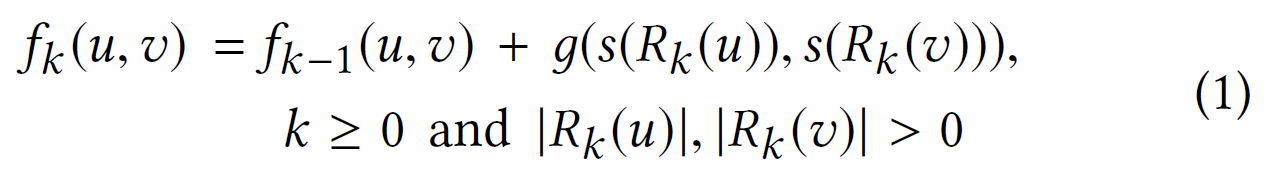
其中$g(D_{1},D_{2})\ge0$表示有序度序列$D_{1},D_{2}$之间的距离,$f_{-1}=0$. 如果$ u $和$ v $的$ k $跳邻域是同构的,并且将$ u $映射到$ v$,则$f_{k-1}(u,v)=0$.
最后还需要定义比较两个度序列之间的函数。两个序列的长度可能不同,其中的元素是$[0,n-1]$之间的随机数。所以可以使用动态时间规整(DTW, Dynamic Time Warping)算法,DTW找出两个序列 A 和 B 之间的最佳比对,定义其中的距离函数:
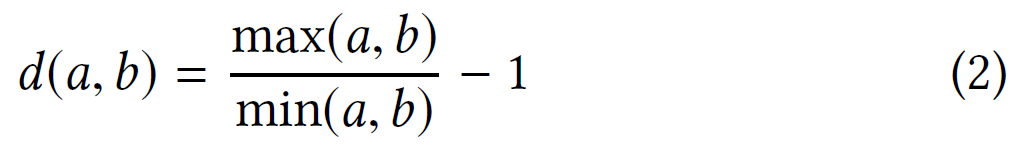
保证当$a=b$的时候$d(a,b)=0$。
2. 构建上下文图 Constructing the context graph
构建了一个多层加权图,对节点之间的结构相似性进行编码。令$M$表示多层图,每一层$k$通过节点的$k$跳邻域定义。
每层$k=0,…,k^{*}$通过一个有权无向完全图进行构造,两点间的边权重为:
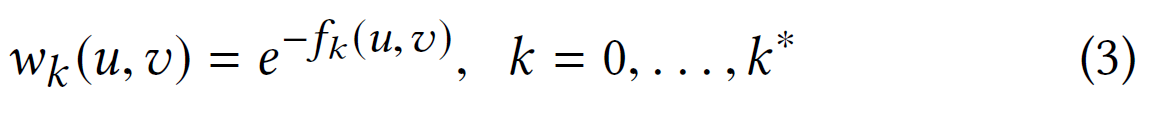
通过有向边连接每层,每个顶点都连接到其上下层中的相应顶点(层许可)。即第$k$层中$u\in V$与$k-1,k+1$层连接的边权重为:
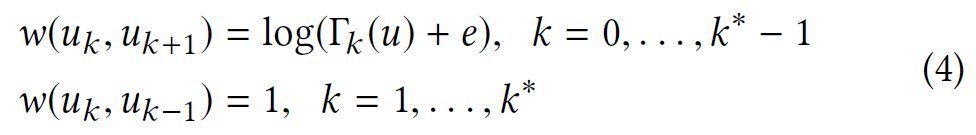
其中$\Gamma_{k}(u)$表示与 u 相关且权重大于第$ k $层中完整图的平均边权重的边数。即:
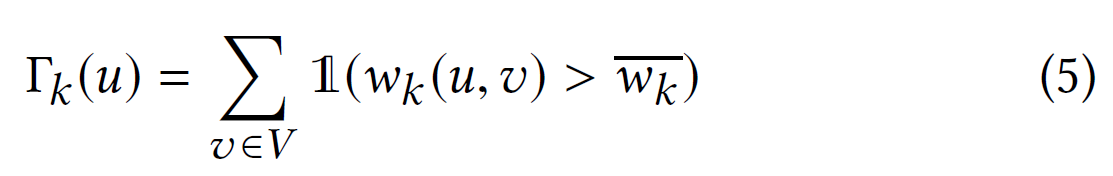
所以,$\Gamma_{k}(u)$可以测量节点$ u $与第$ k $层其他节点的相似度
3. 为节点生成上下文 Generating context for nodes
$M$完全不使用标签信息来捕获 G 中节点之间结构相似性的结构。struct2vec使用随机游走生成节点序列来确定给定节点的上下文。 我们考虑在$ M $周围移动的有偏见的随机游走,根据$ M $的权重做出随机选择。
给定留在当前层的概率$p$,每一步游走之前需要决定是否移动到其他层还是继续在当前层游走。
1. 当前层
在第$ k $层从节点$ u $步进到节点$ v $的概率由下式给出:
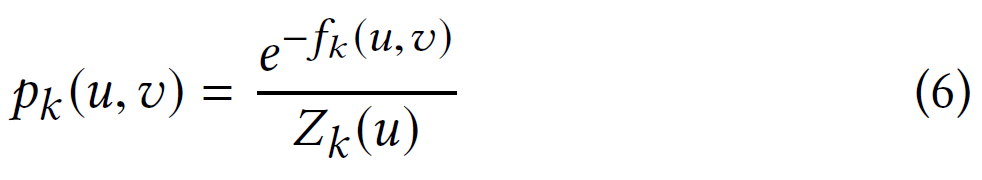
其中,$Z_{k}(u)$是第$ k $层顶点$ u $的归一化因子:
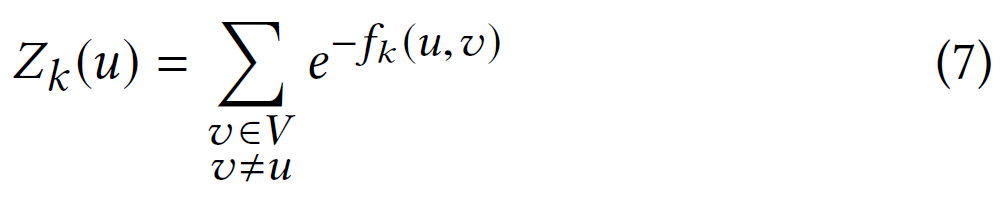
随机游走会更喜欢步入到结构上与当前顶点更相似的节点,避免与当前顶点结构不太相似的节点。因此,节点$u\in V$的上下文可能具有结构相似的节点,独立于它们在原始网络$ G $中的标签和位置。
2. 改变层
如果决定移动到其他层的对应节点,还需要决定是移动到上一层还是下一层,概率为:
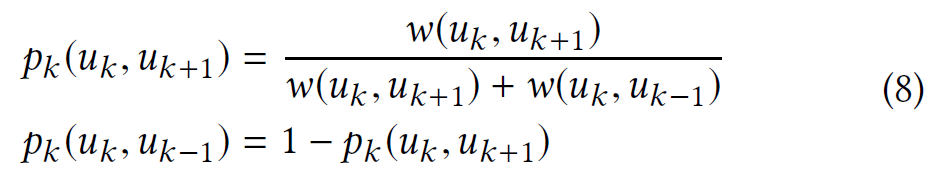
每次 walker 步入一个层时,它都会将当前顶点作为其上下文的一部分,独立于该层。因此,顶点$ u $可能在第$ k $层具有给定的上下文(由该层的结构相似性确定),但在第$ k + 1 $层具有该上下文的子集,因为结构相似性不会随着我们移动到更高层而增加。
最后,对于每个节点$u\in V$,我们在其对应的第0层顶点开始随机游走。随机游走具有固定且相对较短的长度(步数),并且该过程重复一定次数,从而产生到多个独立的步行(即节点$ u $的多个上下文)。