通过简单地增加负样本的数量,最近提出的 ATTH 模型可以在 Temporal KGs (TKGs) 上实现具有竞争力甚至更好的性能,尽管它是非时间性的。 本文进一步提出了 HERCULES,这是 ATTH 模型(2020 ACL)的时间感知扩展,它将黎曼流形的曲率定义为关系和时间的乘积,这是第一次尝试利用流形的曲率来强制时间感知表示。
1. 问题定义
考虑一个有效的四元组$<s,p,o,t>\in S\subset E\times R\times E\times T$,其中$E,R,T,S$分别表示实体集合、关系集合、时间戳集合和事实集合。打分函数$f:E\times R\times E\times T\to R$要求对$\in S$的四元组实现$f(s,p,o,t)$最大化,$\notin S$的四元组最小化。在上述约束的优化过程中,实体、关系和时间的表示被相应地学习,然后,生成的嵌入可以捕获多关系图结构。因此,$f$衡量实体$s$在时间$t$通过关系$p$连接到实体$o$的概率。
2. 双曲几何
欧几里得空间的曲率为零,因此称为平坦空间;双曲几何具有恒定的负曲率。当在双曲空间中表示直线时,直线会变成曲线,称为测地线(如图 1)。
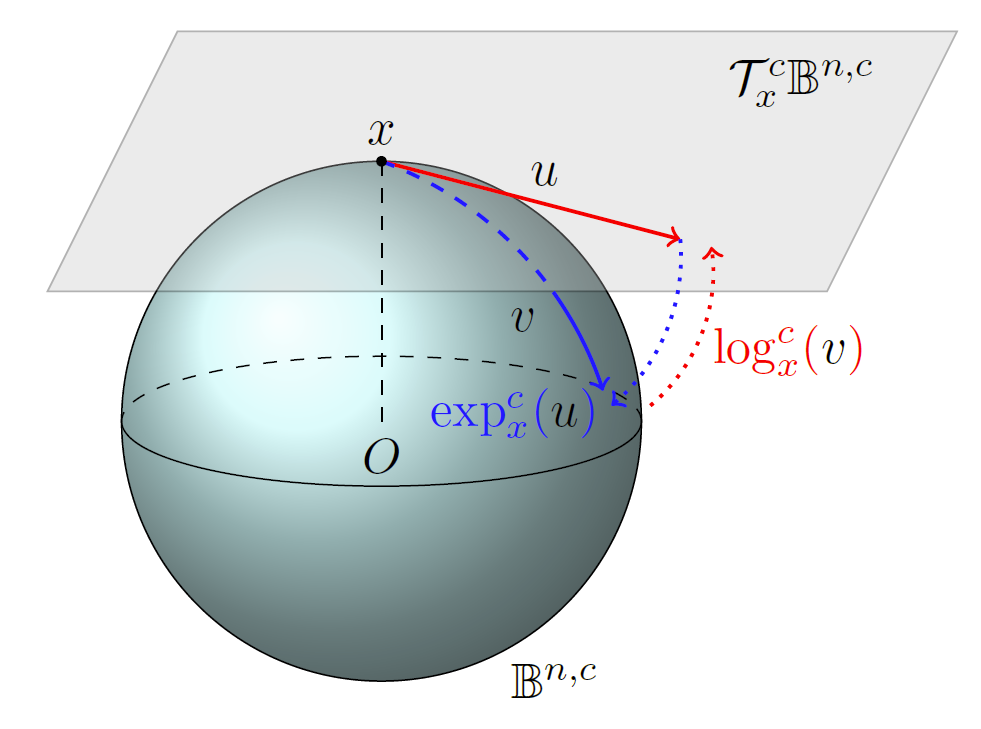
本文同之前在双曲空间进行知识图谱嵌入的模型一样,在庞加莱球中进行。同样通过指数映射和对数映射在双曲空间和正切空间之间进行切换。
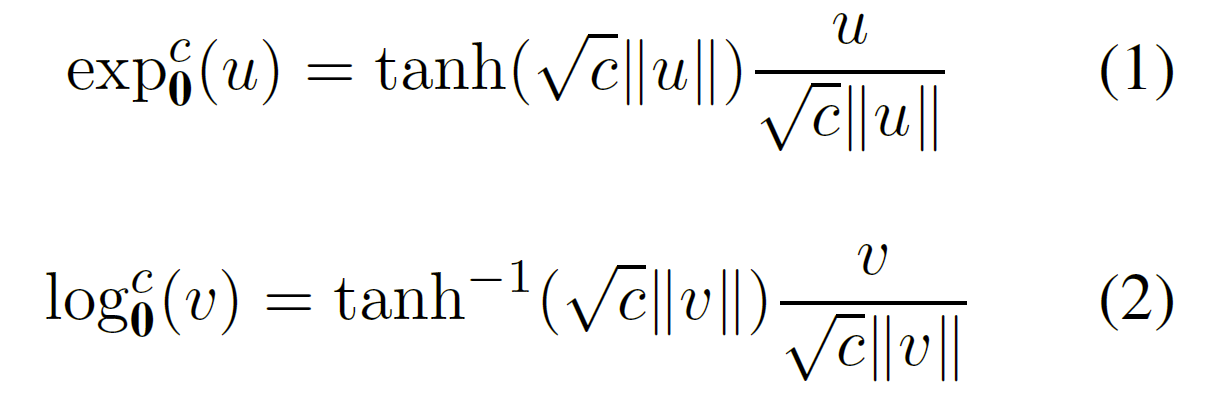
同样为了替换欧几里得加法,本文使用满足流形边界约束的莫比乌斯加法:

进而使用通过莫比乌斯加法定义的双曲距离公式:
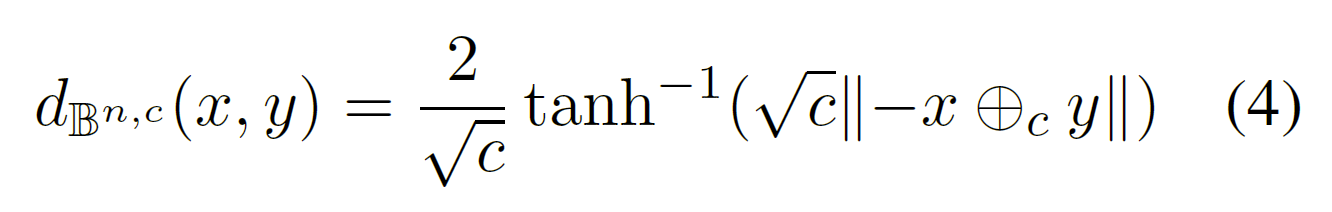
3. 从ATTH到HERCULES
3.1 ATTH
ATTH 使用特定关系的嵌入、旋转、反射和曲率。 曲率定义为取决于所涉及的对应关系$p$。准确地说,关系$ p $被赋予一个单独的参数曲率$c_{p}$:

其中$\mu_{p}$是可训练的参数,$\sigma$是ReLU激活函数的平滑逼近。
通过这种方法,可以学习流形的几何形状,从而针对特定谓词进行修改。 曲率决定了流形的形状, 改变流形的曲率意味着改变投影点的位置。 这意味着对于不同的关系,由于每个关系的不同几何形状,同一实体将具有不同的位置。
为了学习旋转和反射,ATTH使用$2\times 2$的Givens变换矩阵。这些变换在双曲空间中保持相对距离,因此可以直接应用于双曲嵌入(等距)。我们表示$W_{\Theta_{p}}^{rot},W_{\Phi_{p}}^{ref}$为块对角矩阵,对角线上的元素分别通过$G^{+}(\theta_{p,i}),G^{-}(\phi_{p,i})$给出,其中$i$表示对角线中的第$i$个元素:
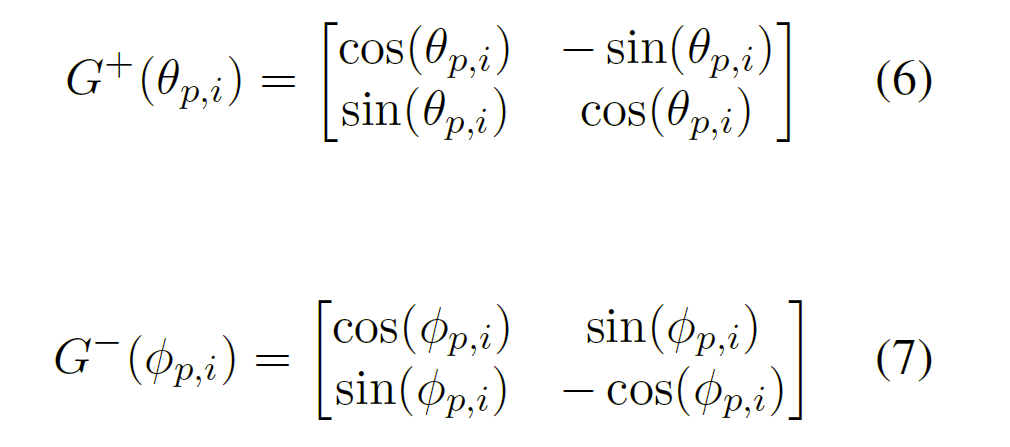
旋转和反射仅应用于主体嵌入:
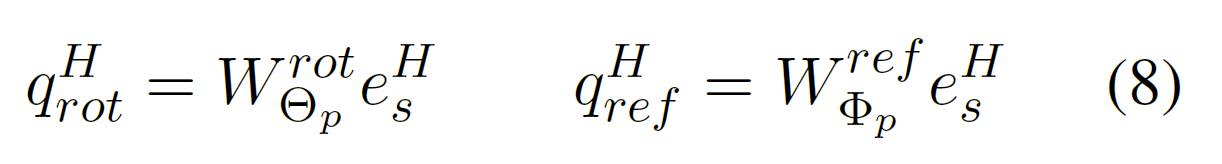
此外,为了表示可以混合旋转和反射的复杂关系,ATTH 使用了双曲线注意力机制。通过指数映射,在正切空间计算注意力分数$\alpha^{p}{q{rot}^{H}},\alpha^{p}{q{ref}^{H}}$;ATTH通过切线空间平均来实现典型的加权平均,之后再通过指数映射回到双曲空间:
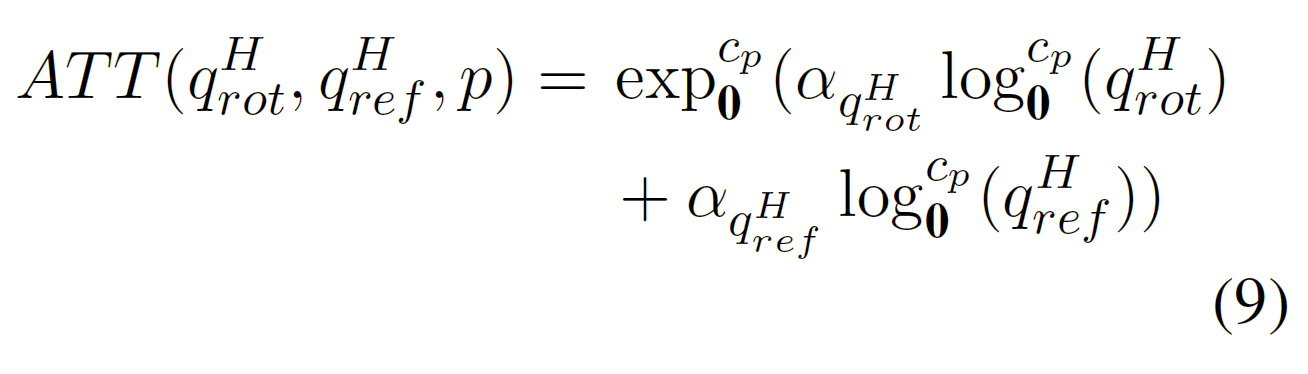
ATTH 最终将一个双曲关系嵌入$r_{p}^{H}$的平移应用到生成的注意力向量上,平移有助于在层次结构的不同级别之间移动。
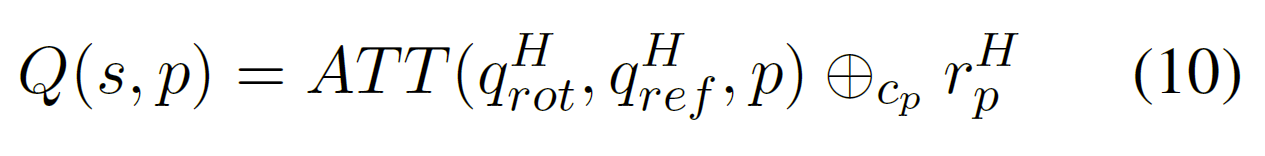
最终的得分函数定义为:
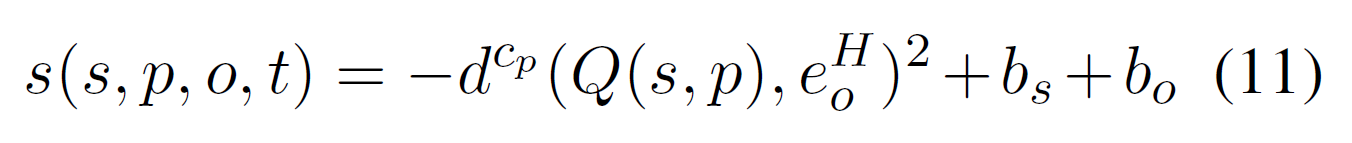
3.2 HERCULES
在ATTH的基础上进一步提出HERCULES,将流形的曲率重新定义为关系和时间的乘积。
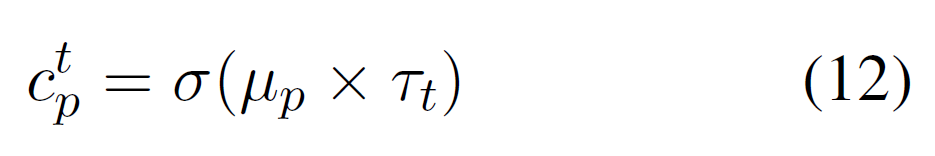
HERCULES 的主要思路是关系和时间都直接调整流形的几何形状,使得投影实体的位置与关系和时间相关。 这是有利的,因为不需要每个实体的附加时间参数。 由于整个几何结构针对特定关系和时间发生了变化,因此该流形上的所有未来投影都将与相应的关系和时间戳对齐。
4. 总结
整篇文章读下来感觉是,重新读了一遍ACL 2020的Low-Dimensional Hyperbolic Knowledge Graph Embeddings,唯一的改进点在于将流形的曲率与关系和时间挂钩,而这篇文章的问题仍然在于没有考虑“时序”,只是将时间戳作为一个特征。