2019 ICML Oral Lorentzian Distance Learning for Hyperbolic Representations
本文的主要贡献是对洛伦兹距离的研究。本文解释了为什么平方洛伦兹距离是比庞加莱度量更好的选择。 一个分析论点依赖于黎曼质心的雅可比场 (Lee, 2006) 特性(也称为“Karcher 均值”,尽管 Karcher (2014) 强烈反对使用该术语)。 另一个有趣的特性是,与平方洛伦兹距离相关的质心可以写成封闭形式,这种质心的欧几里得范数随着双曲空间曲率的减小而减小。此属性适合表示层次结构,其中父节点与其后代的距离最小,并且欧几里得范数小于其子节点。
文章表明用一组点解释平方洛伦兹距离等效于用它们的质心解释距离,同时还研究了质心与一些超参数的相关性,特别是流形的曲率,它会影响其欧几里得范数,该范数用作层次结构中的深度代理。
1. Hyperbolic Background
1.1 Poincare Ball
庞加莱球$P^{d}$被定义为欧几里得范数小于 1 的$d$维向量集:$P^{d}=\lbrace x\in R^{d}:||x||<1\rbrace$.
1.2 Hyperboloid Model
双曲面模型$H^{d,\beta}\in R^{d+1}$也叫洛伦兹模型,定义为:
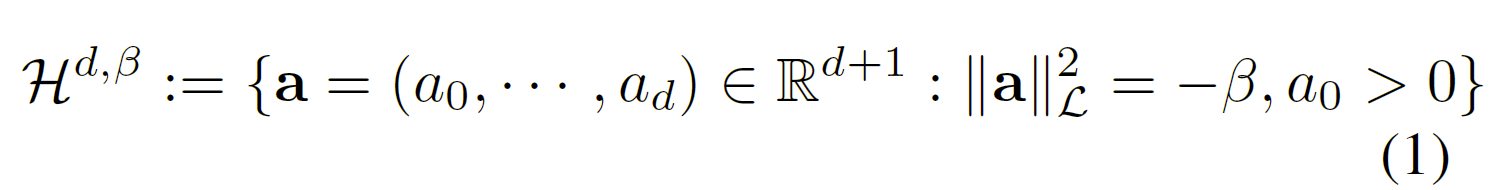
平方洛伦兹范数源自洛伦兹内积:

当$\beta=1$时,双曲面模型称为单位双曲面,可以表示为$H^{d}$,也是文献中考虑的主要双曲面模型。
1.3 Optimizing the Poincare Distance Metric
大多数双曲线表示的方法都考虑庞加莱距离度量:
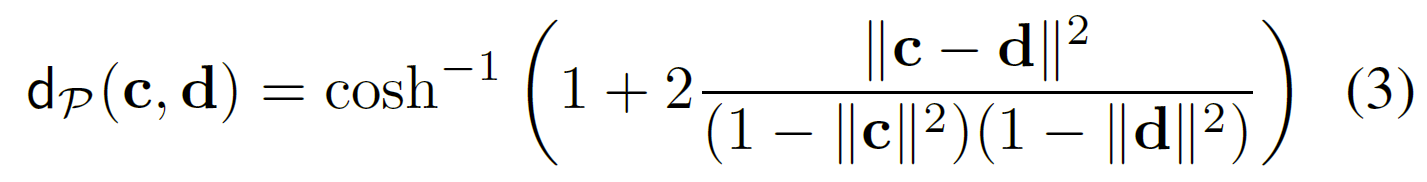
使用方程(3)中的距离公式直接优化问题的庞加莱模型在数值上不稳定,主要有两个原因:
- 分母取决于示例的范数,因此当 c 和 d 的任何一个范数接近 1 时对其进行优化会导致数值不稳定;
- 元素必须在每次迭代时以固定的最大范数重新投影到庞加莱球上;
此外,方程(3)当 $c = d$ 时不可微。
为了获得更好的求解器数值稳定性,Nickel & Kiela (2018) 建议在单位双曲面模型中使用$d_{P}$的等效公式。他们利用存在可逆映射$h:H^{d,\beta}\to P^{d}$的事实:
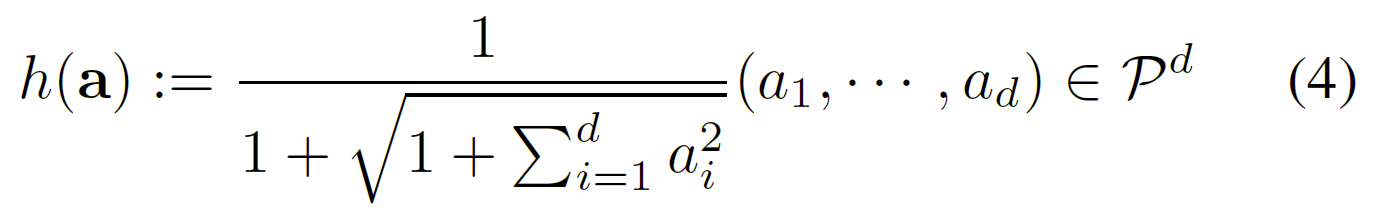
当$\beta=1,a\in H^{d},b\in H^{d}$时,有如下的等价式:
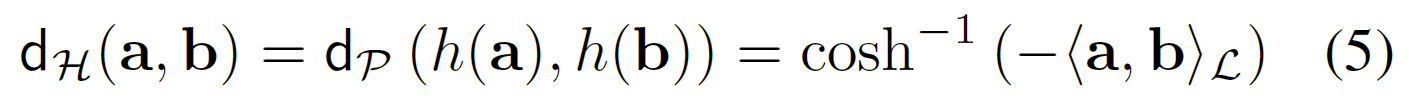
Nickel & Kiela (2018) 表明,(5)中的优化方程在数值上更稳定。
1.5 Duality between Spherical and Hyperbolic geometries 二元性
从方程(5)可以看出,保持Poincare距离的顺序等同于保持Lorentzian内积的逆序,因为$\mathrm{cosh}^{-1}$函数在其域$[1,+\infin]$上单调递增。当$p,q$由于这些几何之间的二元性而位于单位超球面$S^{d}$时,庞加莱度量与洛伦兹内积的关系其实类似于测地距离$\cos^{-1}(<p,q>)$与余弦$<p,q>$的关系。
双曲面$H^{d,\beta}$可以看作是一个虚半径为$i\sqrt{\beta}$的半超球面。 与将 Hilbert 空间中的内积视为相似性度量的核方法相同,本文中考虑洛伦兹内积及其诱导距离。
2. Lorentzian Distance Learning
当表示为双曲时,给出了洛伦兹质心的公式,并表明其欧几里得范数(用作层次结构中的深度代理)取决于曲率$-\frac{1}{\beta}$。
2.1 Lorentzian Distance and Mappings
首先给出平方洛伦兹公式的定义:
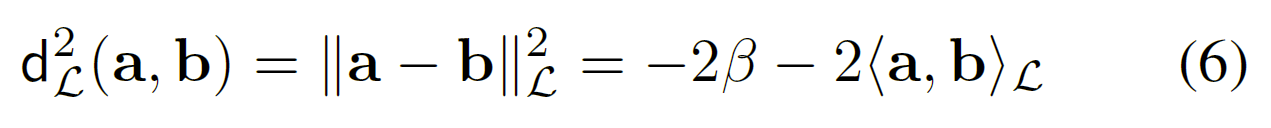
除了三角不等式,它满足距离度量的所有公理。
Mapping 映射
由于我们的方法不一定考虑 β = 1,我们考虑可逆映射$g_{\beta}:F^{d}\to H^{d,\beta}$,称为$H^{d,\beta}$的本地参数化:
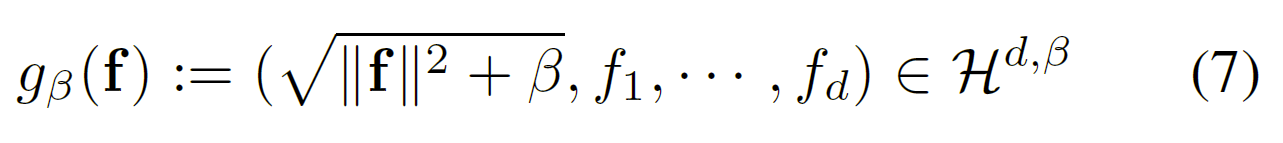
通过平方洛伦兹公式可以比较两个样例$f_{1},f_{2}\in F^{d}$:
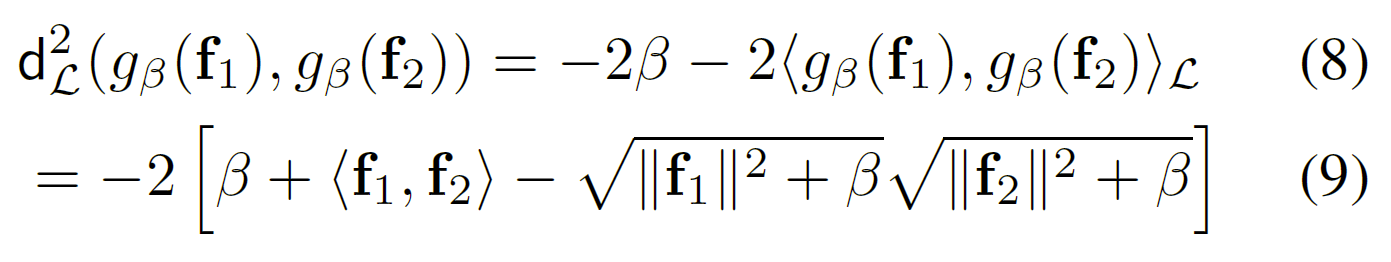
Preserved order of Euclidean norms 欧几里得范数的保留顺序
示例的欧几里得范数的顺序沿三个空间保留,可由以下定理给出:

总之,示例的欧几里得范数可以在任何空间中等价地进行比较,如果想研究质心的欧几里得范数,这特别有用。
2.2 Centroid Properties 质心属性
质心是 (Frechet, 1948) 中提出的统计概念,用于估计一组点的某些统计离散度(例如方差),它是一组点的(平方)距离期望的最小值,并在 (Grove & Karcher, 1973) 中扩展到黎曼流形。研究平方洛伦兹距离的质心,在理想情况下,希望节点表示的质心是(接近)其最低共同祖先的表示。
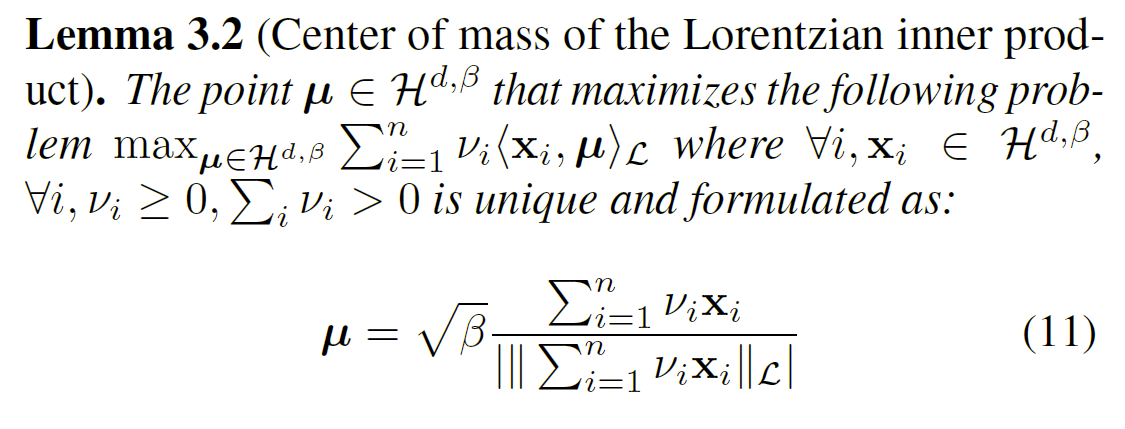
公式 (11) 中的质心公式概括了 (Galperin, 1993; Ratcliffe, 2006)中给出的质心公式,适用于任何数量的点和任何恒定曲率 -1/β 的值。
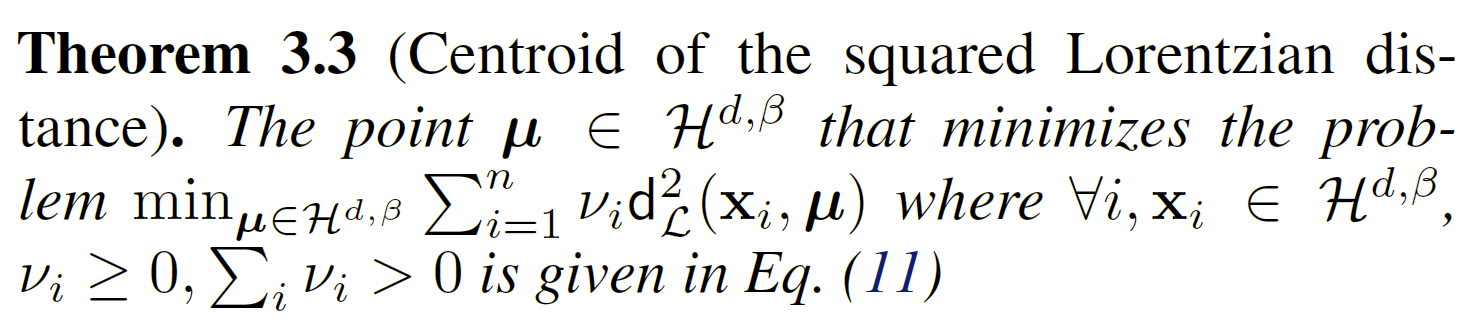
质心 μ 的公式可用于执行硬聚类,其中假设对聚类中的数据采用统一度量。可以看到,一个示例的质心就是示例本身。
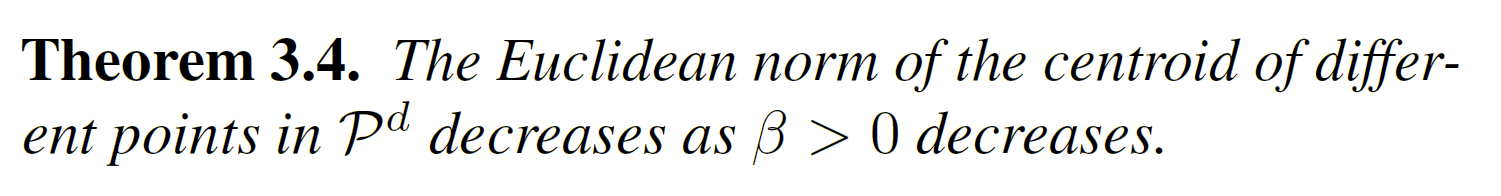
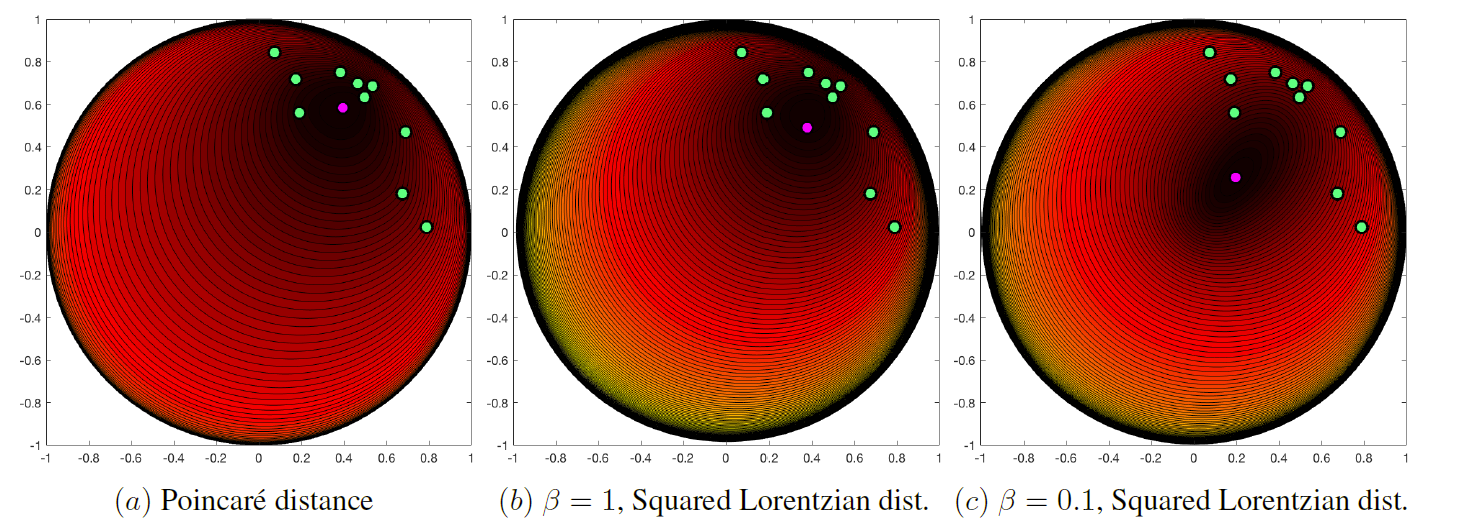
图 1 说明了一组 10 个不同点的质心的二维庞加莱球表示。不同 β > 0 值的庞加莱距离和平方洛伦兹距离。可以看到质心庞加莱度量没有更小的范数。 另一方面,洛伦兹质心的欧几里得范数确实随着 β 的减小而减小,然后可以通过选择 β > 0 的较低值来强制使其变小。
下面提供了一些有助于理解洛伦兹距离的旁注。
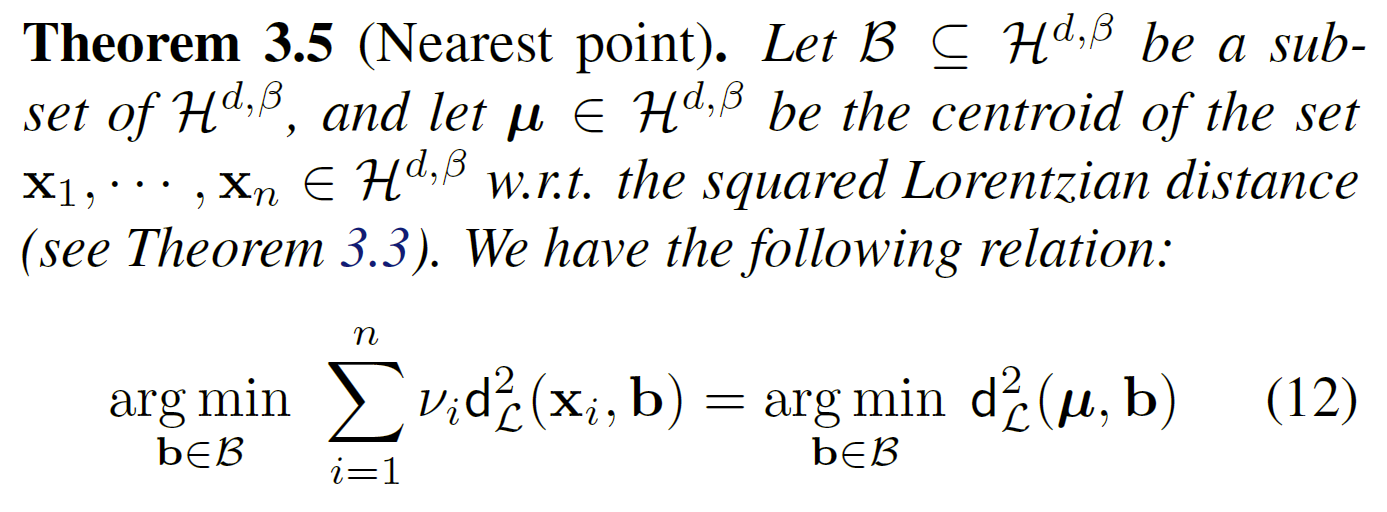
该定理表明,一组点的距离只能与作为质心的一个点进行比较。
此外,根据柯西-施瓦茨不等式,当 β 趋于 0 时,方程 (9) 中的洛伦兹距离到$f_{1}$的任何向量$f_{2}$都趋于 0,其可写为$f_{2}=\tau f_{1}$且$\tau\ge 0$,否则距离更大。因此,具有一组点的洛伦兹距离沿着包含可以写为τμ的元素的射线趋于更小,其中τ ≥ 0且 μ 是它们的质心。 $$ (\sum_{k=1}^{n}{a_{k}\cdot b_{k}})^{2}\le (\sum_{k=1}^{n}{a_{k}^{2}})(\sum_{k=1}^{n}{b_{k}^{2}})\ $$
Curvature adaption 曲率适应
根据雅可比场性质,当所选度量是单位双曲面$H^{d}$上的庞加莱度量$d_{H}$时,$d_{H}$的Hessian沿径向具有特征值0。然而,Hessian 的特征值是水平面的主曲率。 由于矢量场更重要并且为了获得“更好的曲率适应”(Karcher,2014)(即非零特征值),Karcher (1987) 建议使用“修正距离”$(-1+\cosh(d_{H}))$,它在$H^{d}$上等于$\frac{1}{2}d_{L}^{2}$.
Hyperbolic centroids in the literature 双曲质心
有另外两篇论文利用了双曲质心。 首先是萨拉等人 (2018) 使用与 Poincare 度量相关的质心,但没有封闭形式的解决方案,因此他们通过梯度下降来计算它。 古尔切尔等人 (2019) 优化了一个基于庞加莱度量的问题,但利用了属于另一种双曲几何类型的陀螺质心 (Ungar, 2014)。 当该集合仅包含 2 个点时,它是使用陀螺三角不等式将其与该集合的两个点之间的陀螺距离进行爱因斯坦加法的最小值。 否则,可以将其视为保留左回旋平移的点。 陀螺质心的一个限制是它不能被视为距离期望的最小值(与 Frechet 均值不同),因为爱因斯坦加法不是可交换的。
2.3 Optimization and solver
$d_{H}$的方向导数缺乏合适的向量空间结构,无法使用标准优化器。另一方面,平方洛伦兹距离仅依赖于方程(2)中洛伦兹内积的公式,该公式对于任何对都是明确且平滑的。通过尝试减少向量空间中的洛伦兹距离,标准 SGD 也减少了测地距离。