2020 ACL会议《A Joint Neural Model for Information Extraction with Global Features》
该论文提出一个名为ONEIE的信息抽取框架,增加一个全局特征,在实例之间和子任务之间进行联合决策。
1. Introduction
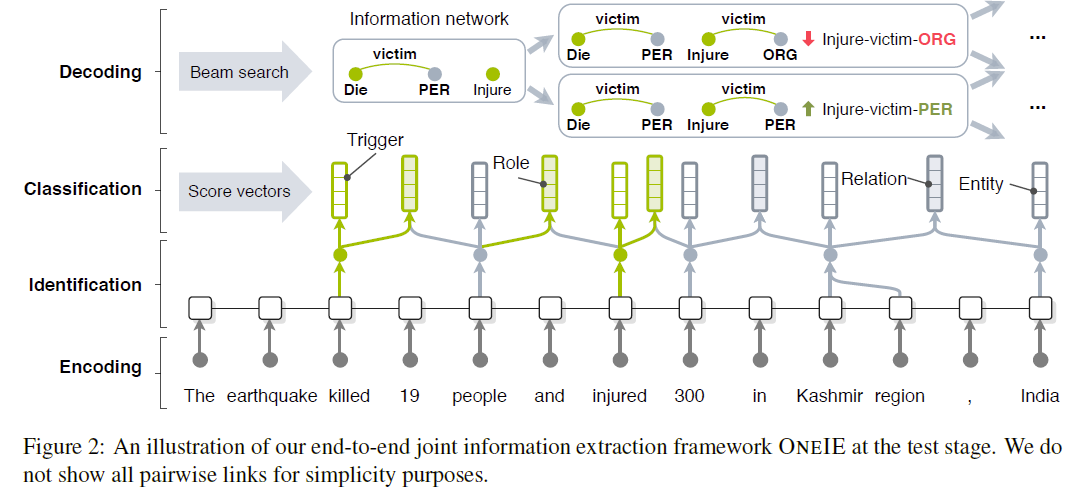
大多数的信息抽取的联合学习模型使用task-specific分类对独立实体进行标记而不是使用实体之间的交互信息。论文提出名为ONEIE的端到端信息抽取框架,整个过程分为四个操作阶段:
- 对输入语句进行编码(Embedding);
- 识别句中的实体(Entity)和事件(Event)并用结点(Node)进行表示;
- 使用句内信息(Local classifier)计算所有结点及其连接(Link)的标签分数(Label Score);
- 解码(Decoding)时使用束搜索(Beam search)找到全局最优图。
在解码阶段加入全局特征(Global Feature)捕捉实例之间(cross-instance)和子任务之间(cross-subtask)的联系(Interaction)。同时ONEIE框架没有使用任何特定语言的语法特征(Language-specific feature),所以很容易适应新语言。
2. Task
-
Entity Extraction 实体抽取
根据提前定义(Pre-defined)的实体分类识别语句中提及的实体。
-
Relation Extraction 关系抽取
对给定的实体对分配关系类型。
-
Event Extraction 事件抽取
涉及识别非结构语句中的事件触发语(Event trigger: the word or phrases that most clearly express event occurrences)及这些词语和短语的论据(Arguments: the words and phrases for participants in those events),并将这些短语根据类型和语法规则进行分类。
一个Argument可以是一个实体、时间表达式或数值等。
对信息抽取的任务作如下规定: 对于给定的句子,目的是提取一个信息表示图:$G=(V,E)$,其中$V$和$E$分别表示结点集和边集。
对于任意结点$v_i=<a_i, b_i, l_i>\in V$表示一个实体(Entity)或事件触发器(Event trigger),其中$a$和$b$分别表示结点起始和结束词语的索引(indices),$l$表示结点类型标签(Node type label)。
对于任意边$e_{ij}=<i,j,l_{ij}>\in E$表示两个结点之间的关系,其中$i$和$j$分别表示两个相关结点的索引,$l_{ij}$表示关系类型。
3. Approach
ONEIE框架对给定的语句进行信息网络提取,分为以下四步:encoding,identification,classification和decoding。我们使用预训练的BERT模型进行编码,然后对语句中的实体和事件触发器进行识别。之后计算所有的结点和相关的边的类型标签分数(Type label scores)。在解码阶段,我们使用束搜索(Beam Search)探索输入语句可能的信息网络。
3.1 Encoding
输入一句包含$L$个词的语句,使用预训练的BERT模型将每个词表示为$x_i$。实验发现使用最后三层BERT在大多数的子任务上表现较好。
3.2 Identification
这一阶段将识别句中的实体提及和事件触发器,并表示为信息网络中的结点。我们使用前馈神经网络FFN计算每个词的分数向量$\hat{y}_i=FFN(x_i)$,$\hat{y}_i$表示一个标签在目标标签集(Target tag set)中的分数。
之后使用CRF层捕捉标签之间的联系,计算tag path: $\hat{z}={\hat{z_1},…,\hat{z}_L}$ 的分数:
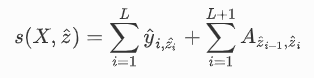
其中$X={x_1,…,x_L}$是输入语句中每个词的向量表示,$\hat{y}{i,\hat{z_i}}$ 是分数向量 $\hat{y}i$在第 $\hat{z}i$条路径的组合,$A{\hat{z}{i-1},\hat{z}{i}}$ 是矩阵A中 $\hat{z}_{i-1}$到 $\hat{z}_i$的转移分数。同时,我们在A中添加两个特殊的标签$
训练阶段时,我们最大化标准标签路径的对数似然估计: $$ \log{p(z|X)}=s(X,z)-log{\sum_{\hat{z}\in Z}{e^{s(X.\hat{z})}}} $$
其中$Z$是输入语句中所有可能标签路径的集合。
所以我们定义实体识别阶段的损失函数为: $$ L^I=-\log{p(z|X)} $$
3.3 Classification
将每个识别出的结点表示为$v_i$,之后使用分离的针对特定任务的前馈神经网络来计算每个结点的标签分数: $$ \hat{y}_{i}^{t}=FFN^t(v_i) $$
其中$t$表示一个特定的任务。
为了获得$i-th$和$j-th$结点之间边的标签分数,我们连接它们的跨度表示(Span Representation),将向量表示为: $$ \hat{y}_{k}^{t}=FFN^t(v_i,v_j) $$
对于每个任务,训练目标是最小化以下交叉熵损失: $$ L^{t}=-\frac{1}{N^t}\sum_{i=1}^{N^t}{y_i^{t}\log{\hat{y}^{t}_{i}}} $$
其中,$y_i^{t}$是向量的正确标签,$N^t$是任务$t$中的实体数量。
如果忽略结点和边的内在依赖关系(Inter-dependencies),我们可以直接通过每个任务的最高分数来预测标签,之后生成局部的最佳图$\hat{G}$。最佳图$\hat{G}$分数的计算方法为: $$ s'(\hat{G})=\sum_{t\in T}\sum_{i=1}^{N^t}{\max{\hat{y}_i^t}} $$
其中,$T$是任务的集合,将$s'(\hat{G})$作为$\hat{G}$的局部分数参考。
3.4 Global Features
我们考虑框架中的两种类型的内部依赖:
-
子任务间的作用 Cross-subtask interactions
这种依赖关系存在于实体、关系和事件之间;
-
实体之间的作用 Cross-instance interactions
这种依赖存在于一个句子中多个事件和/或关系的实例之间。

我们设计一套全局特征类型模板(Event schemas)来捕捉以上两类相互作用,模型填充所有可能的类型来生成特征,并在训练过程中学习每个特征的权重。对于给定的一张图,我们将它的全局特征向量描述为: $$ f_G={f_1(G),…,f_M(G)} $$ 其中,$M$是全局特征的数量,$f_i(\cdot)$是一个函数,对某个特征求值并返回标量。比如: $$ f_i(G)=\begin{cases} 1,G,has,multiple,ATTCK,events\ 0,otherwise \end{cases} $$ 之后,ONEIE框架学习到一个权重向量$u\in \R^{M}$并且将$f(G)$和$u$的点乘作为图G的全局特征分数。将图G的局部分数和全局特征分数之和作为G的全局分数: $$ s(G)=s'(G)+{u}{f}(G) $$ 我们假定一条语句的最佳(Gold-standard)图应该拥有最高的全局分数。所以,我们最小化该损失函数: $$ L^{G}=s(\hat{G})-s(G) $$ 其中,$\hat{G}$是局部分类得到的图,$G$是最佳图。
最终,我们在训练中最优化如下的联合目标函数: $$ L=L^I+\sum_{t\in{T}}{L^t}+L^{G} $$
3.5 Decoding
ONEIE对所有的结点和成对的边进行联合决策,得到全局的最优图。最基本的方法是计算所有候选图的全局分数,选择分数最高的作为最终结果。为了优化复杂度,我们设计了一个以束搜索为基础的解码器(Beam search-based decoder)。
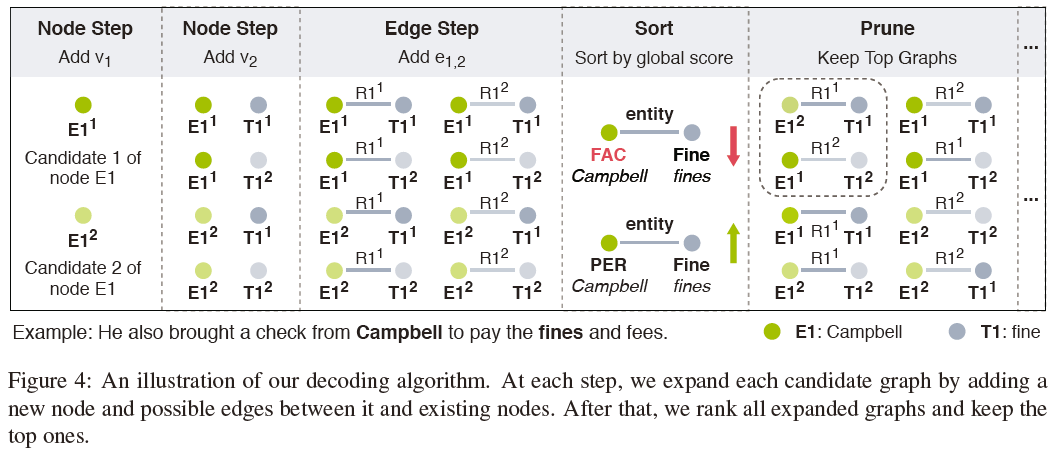
对于给定的识别出的结点集$V$、所有结点的标签分数(label scores)和他们之间的成对联系执行解码,初始束集(initial beam set)为$B={K_{0}}$,$K_0$是一个零阶图。每一步$i$分为两小步,分别对结点和边进行扩展:
-
Node Step
选择$v_i\in V$,定义候选集为$V_i={<a_i,b_i,l_i^{(k)}>|1\le K\le\beta_v}$,其中$l_i^{(k)}$表示$v_i$中分数第$k$高的局部标签分数,$\beta_v$是控制候选标签数量的超参数(hyper-parameter)。通过如下公式更新束集(beam set): $$ B\leftarrow{G+v|(G,v)\in B\times V_i} $$
-
Edge Step
迭代地选择一个$i$之前的结点$v_j\in V,j<i$,同时在$v_j$和$v_i$之间添加可能的边。如果$v_i$和$v_j$都是触发器(trigger)则跳过$v_j$。每一次迭代中,我们构造一个候选边集$E_{ij}={<j,i,l_{ij}^{(k)}>|1\le k\le \beta_e}$,其中$l_{ij}^{(k)}$是$e_{ij}$中分数第$k$高的标签,$\beta_e$是候选标签数量的阈值。之后,通过如下函数更新束集: $$ B\leftarrow {G+e|(G,e)\in B\times E_{ij}} $$ 在每次edge step的最后,如果$|B|$超过束的宽度$\theta$,我们对候选对象按全局分数从高到低进行排序,只保留分数最高的$\theta$个。
最后一步之后,返回全局分数最高的图,作为输入语句中提取的信息网络。
$$ u\in \R^{M} $$