Non-invasive Self-attention for Side Information Fusion in Sequential Recommendation
顺序推荐系统旨在根据用户的历史行为对用户不断变化的兴趣进行建模,从而做出与时间相关的定制推荐。本文提出了 NOninVasive self-Attention 机制 (NOVA) 以在 BERT 框架下有效地利用边信息。 NOVA 利用辅助信息来生成更好的注意力分布,而不是直接改变物品嵌入,这可能会导致信息过多。
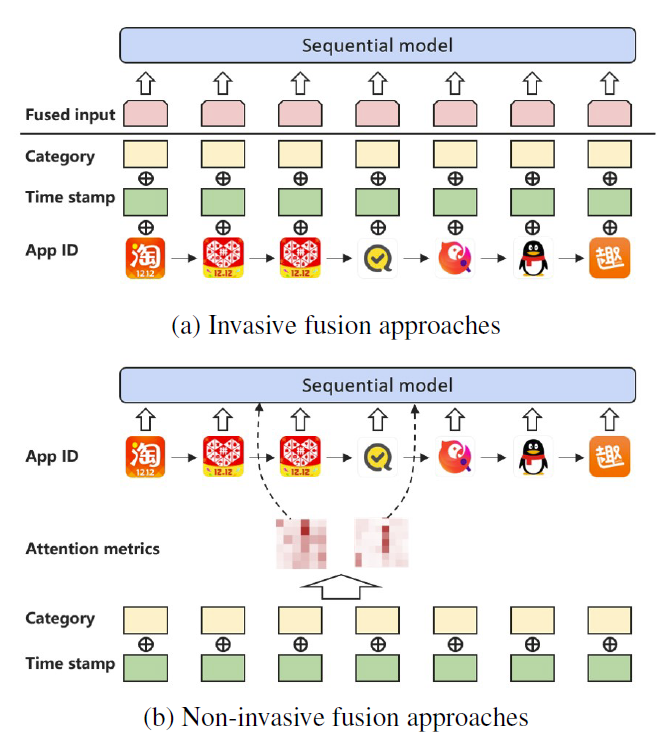
本文研究了如何在成功的 BERT 框架下有效利用各种辅助信息,提出了 NOVA,它可以通过辅助信息持续提高预测精度,并在所有的实验中实现最先进的性能。 如图 1 所示,在 NOVA 中,辅助信息作为自注意力模块的辅助来学习更好的注意力分布,而不是被融合到物品表示中,这可能会导致信息压倒性等副作用。
本文主要贡献:
- 提出了 NOVA-BERT 框架,它可以有效地将各种辅助信息用于顺序推荐任务;
- 提出了非侵入性自注意力(NOVA)机制,这是一种新颖的设计,可以对复合顺序数据进行自注意力;
- 进行详细的实验和部署以证明 NOVA-BERT 的有效性,包括可视化分析以获得更好的可解释性。
1. 相关工作
在顺序推荐领域,充分利用边信息来提高准确率也是一个长期讨论的话题。 如表 1 所示,在 CNN、RNN、注意力模型和 BERT 等不同框架下,之前的一些工作试图利用边信息。 尽管如此,他们中的大多数都使用了辅助信息,而没有过多研究如何添加辅助信息。 几乎所有人都使用一种我们称之为“侵入性”融合的简单做法。

Invasive approaches
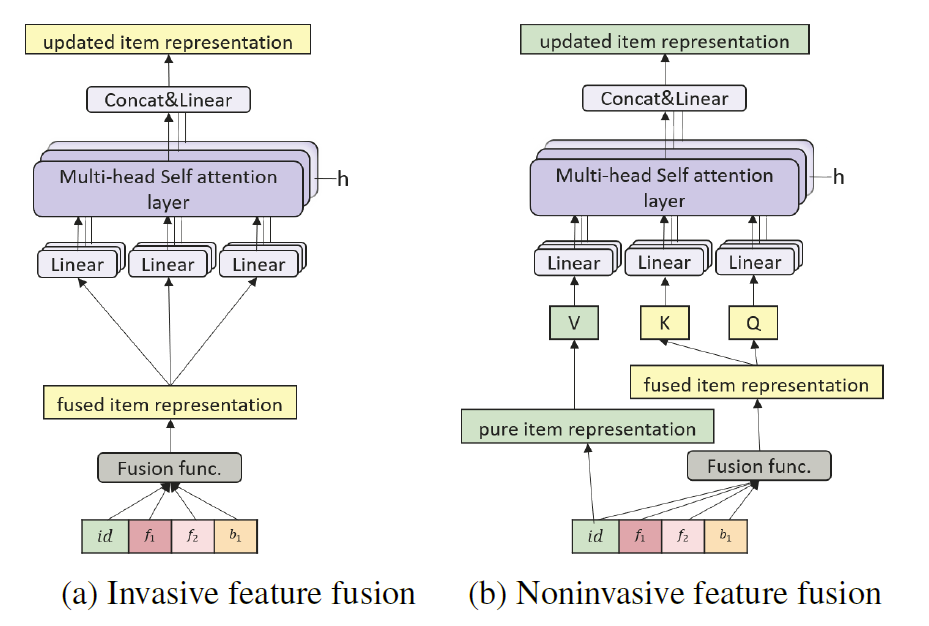
大多数以前的工作,直接将边信息融合到物品表示中,如图 1(a) 所示。 他们通常使用融合操作(例如,求和、串联、门控求和)将额外信息与物品 ID 信息合并,然后将混合物输入神经网络。我们称这种直接合并做法为“侵入性方法”,因为它们改变了原始表示。
如表 1 所示,之前的 CNN 和 RNN 工作试图通过将边信息直接融合到具有连接和加法等操作的物品嵌入中来利用边信息。 GRU等其他一些作品提出了更复杂的特征融合门机制和其他训练技巧,试图使特征选择成为一个可学习的过程。 然而,根据他们的实验结果,简单的方法不能有效地利用各种场景下的丰富边信息。 尽管可以通过为每种类型的辅助信息部署并行子网来提高预测精度,但该模型变得繁琐且不灵活。
另一项研究没有直接改变物品嵌入,而是通过称为物品提升的技巧包括 RNN 模型的停留时间。 一般的想法是让损失函数知道停留时间。 用户查看物品的时间越长,他/她就越感兴趣。 然而,这个技巧在很大程度上依赖于启发式,并且仅限于与行为相关的辅助信息。 另一方面,一些与物品相关的辅助信息(例如价格)描述了物品的内在特征,这些特征不像停留时间那样容易被这种方法利用。
2. 论文模型
本节中详细介绍研究领域和方法论。在第 3.1 至 3.3 节中,指定了研究问题并解释了辅助信息、BERT 和自注意力。然后,在第 3.4 节中介绍了非侵入性自注意力和不同的融合操作。最后,NOVA-BERT 模型在第 3.5 节中进行了说明。
2.1 问题陈述
给定用户与系统的历史交互,顺序推荐任务会询问下一个将与之交互的物品,或者将执行下一个操作。 让 u 表示一个用户,他/她的历史交互可以表示为一个时间序列:

其中$v_{u}^{(j)}$表示用户制造的第$j$个交互(行为),例如下载一个APP。当只有一种类型的动作且没有辅助信息时,每个交互都可以简单地用一个物品 ID 来表示: $$ v_{u}^{(j)}=ID^{(k)} $$ 其中$ID^{(k)}\in I$,表示第$k$个物品的ID。 $$ I=\lbrace ID^{(1)},ID^{(2)},…,ID^{(m)}\rbrace $$ 是系统中要考虑的所有物品的词汇表。 $m$表示词汇量大小,表示问题域中的物品总数。
给定用户$S_{u}$的历史记录,系统预测用户最有可能与之交互的下一个物品:
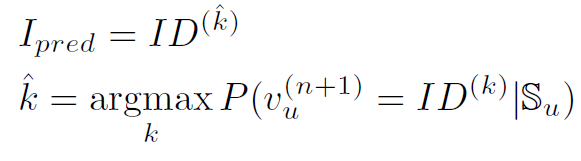
2.2 Side Information 侧面信息
辅助信息可以是为推荐提供额外有用信息的任何内容,可以分为两种类型,物品相关或行为相关。 除了物品 ID(例如,价格、生产日期、生产商)之外,与物品相关的辅助信息是内在的并且描述了物品本身。 与行为相关的辅助信息与用户发起的交互有关,例如操作类型(例如,购买、费率)、执行时间或用户反馈分数。 每次交互的顺序(即原始 BERT 中的位置 ID)也可以作为一种行为相关的辅助信息。
如果涉及辅助信息,则交互变为:
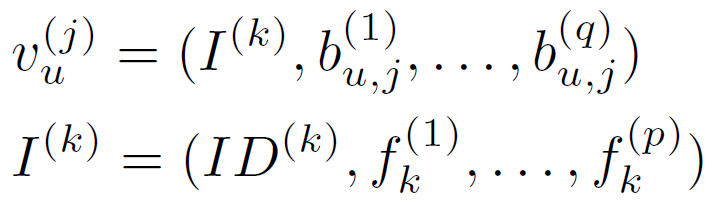
其中$b_{u,j}^{(\cdot)}$表示用户u进行的第$j$次交互的行为相关边信息。$I^{(\cdot)}$表示一个物品,包含一个 ID 和几条物品相关的边信息$f_{k}^{(\cdot)}$。与物品相关的辅助信息是静态的,并存储每个特定物品的内在特征。 因此,词汇表可以改写为:
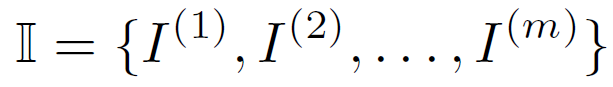
目标仍然是预测下一个物品的 ID:
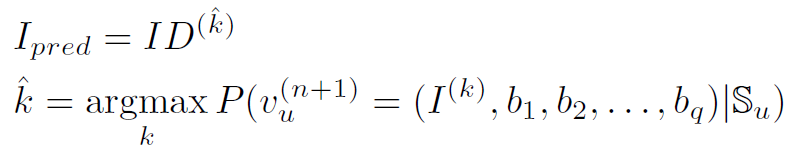
其中$b_{1},b_{2},…,b_{q}$是潜在的与行为相关的边信息,如果考虑与行为相关的边信息。注意到模型应该仍然能够预测下一个物品,而不管与行为相关的辅助信息是假设的还是被忽略的。
2.3 BERT 和 Invasive Self-attention
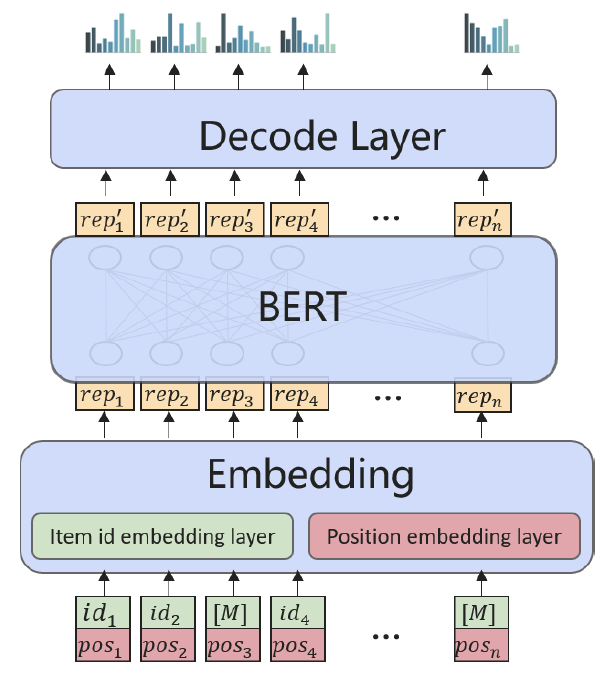
BERT4Rec (Sun et al. 2019) 是第一个将 BERT 框架用于顺序推荐任务的方法,实现了 SOTA 性能。 如图2所示,在BERT框架下,物品被表示为向量,称为embeddings。 在训练期间,一些物品被随机屏蔽,BERT 模型将尝试使用多头自注意力机制(Vaswani et al. 2017)恢复它们的向量表示和物品 ID:
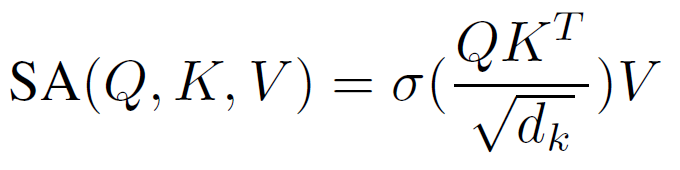
其中$\sigma$是 softmax 函数,$d_{k}$是比例因子,$Q$、$K$和$V$是查询、键和值的派生分量。 BERT 遵循编码器-解码器设计,为输入序列中的每个物品生成上下文表示。 BERT 使用嵌入层来存储 m 个向量,每个向量对应于词汇表中的一个物品。
为了利用边信息,传统方法使用单独的嵌入层将边信息编码为向量,然后将它们融合到具有融合函数$F$的 ID 嵌入中。 方法将边信息注入原始嵌入,并生成混合表示:
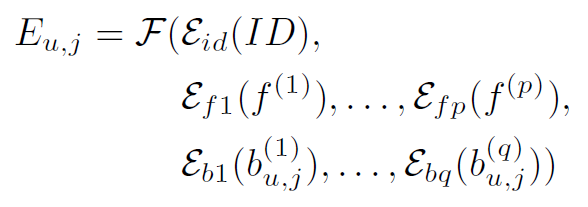
其中$E_{u,j}$是用户$u$第$j$次交互的集成嵌入,$E$是将对象编码为向量的嵌入层。 集成嵌入的序列作为用户历史的输入输入模型。
BERT 框架将通过自注意力机制逐层更新表示:
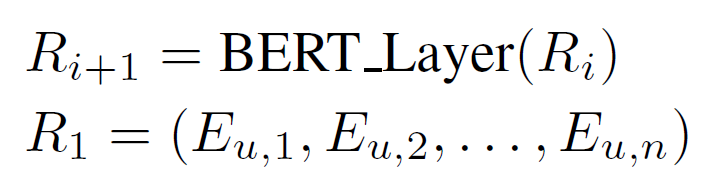
在最初的BERT和Transformer中,self-attention 操作是一个位置不变函数。 因此,每个物品嵌入都添加了一个位置嵌入来显式地对位置信息进行编码。 位置嵌入也可以被视为一种与行为相关的辅助信息(即交互的顺序)。 从这个角度看,原来的BERT也是把位置信息作为唯一的边信息,用加法作为融合函数F。
2.4 NOVA
如果端到端地考虑 BERT 框架,它是一个具有堆叠自注意力层的自动编码器。 相同的嵌入映射用于编码物品 ID 和解码恢复的向量表示。 因此认为侵入性方法具有复合嵌入空间的缺点,因为物品 ID 与其他辅助信息不可逆转地融合。 混合来自 ID 的信息和其他辅助信息可能会使模型不必要地难以解码物品 ID。
因此提出了一种称为无创自注意力(NOVA)的新方法,以保持嵌入空间的一致性,同时利用边信息更有效地对序列进行建模。 这个想法是修改自注意力机制并仔细控制自注意力组件的信息源,即查询 Q、键 K 和值 V (Vaswani et al. 2017)。 除了第 2.3 节中定义的集成嵌入 E,NOVA 还保留了一个用于纯 ID 嵌入的分支:
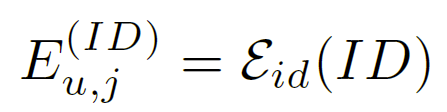
因此,对于 NOVA,用户历史现在由两组表示组成,纯 ID 嵌入和集成嵌入:
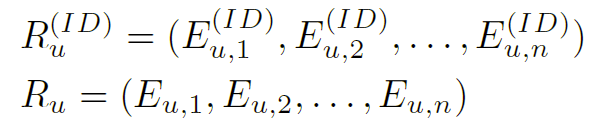
NOVA 从集成嵌入 R 计算 Q 和 K,从物品 ID 嵌入$E^{(ID)}$计算 V。实际中,以张量形式处理整个序列,其中 B 是批量大小,L 是序列长度,h 是嵌入向量的大小。NOVA 可以形式化为:
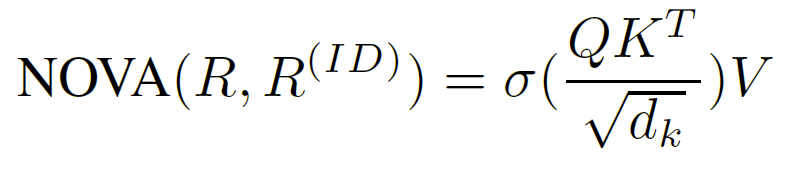
用线性变换计算的 Q、K、V:
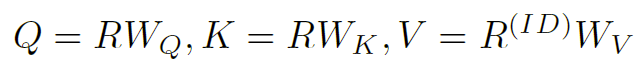
NOVA 和侵入式辅助信息融合方式的比较如图 3 所示。 一层一层地,沿着 NOVA 层的表示保持在一个一致的向量空间内,完全由物品 ID 的上下文形成。
2.5 融合操作
NOVA 以不同于侵入式方法的方式利用边信息,将其视为辅助信息,并使用融合函数 F 将边信息融合到 Keys 和 Queries 中。在这项研究中,我们还研究了不同类型的融合函数及其性能。
如上所述,位置信息也是一种行为相关的边信息,原始BERT利用它的加法操作很简单:
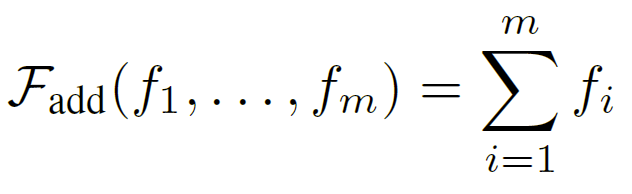
此外,定义了“concat”融合器来连接所有边信息,然后是一个完全连接的层来统一维度:
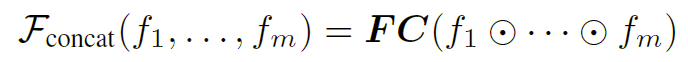
此外,还设计了一个门控融合器,其可训练系数来自上下文:
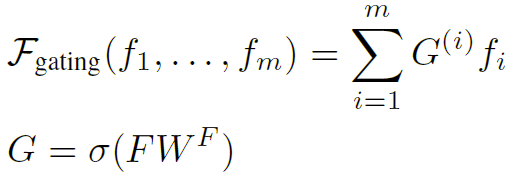
其中$F$是所有特征的矩阵形式$[f_{1},…,f_{m}]\in R^{m\times h}$,$W^{F}\in R^{h\times1}$是可训练的参数,$h$是要融合的特征向量的维度。
2.6 NOVA-BERT
如图 4 所示,在 BERT 框架下使用 NOVA 操作实现了 NOVA-BERT 模型。 每个 NOVA 层接受两个输入,补充边信息和物品表示序列,然后输出相同形状的更新表示,这些表示将被馈送到下一层。 对于第一层的输入,物品表示是纯物品 ID 嵌入。 由于仅使用辅助信息作为辅助来学习更好的注意力分布,因此辅助信息不会与 NOVA 层一起传播。 为每个 NOVA 层明确提供了相同的辅助信息集。
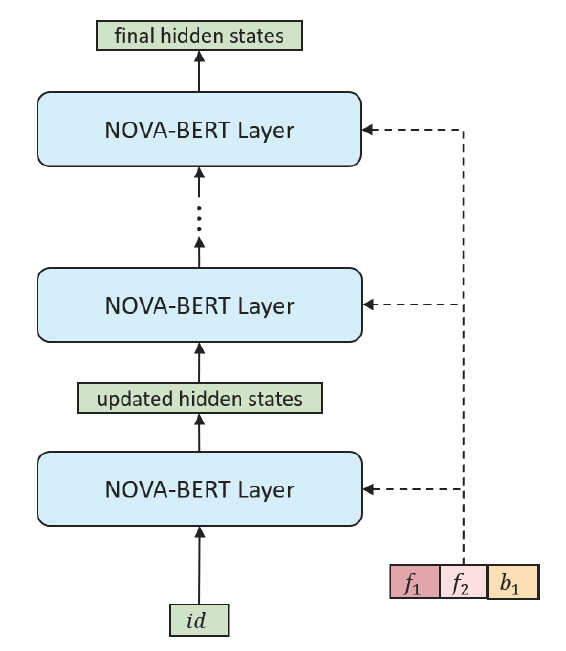
NOVA-BERT 遵循 (Devlin et al. 2018) 中原始 BERT 的架构,除了用 NOVA 层替换 self-attention 层。 因此,额外的参数和计算开销可以忽略不计,主要由轻量级融合函数引入。
使用 NOVA-BERT,隐藏的表示被保存在相同的嵌入空间中,这将使解码过程成为同构向量搜索并有利于预测。 下一节的结果也实证验证了 NOVA-BERT 的有效性。