Improving Collaborative Metric Learning with Efficient Negative Sampling (arxiv.org)
基于三元组损失的距离度量学习已成功应用于广泛的应用中,例如人脸识别、图像检索、说话人变化检测以及最近使用协作度量学习 (CML) 模型进行推荐。然而,正如我们在本文中所展示的,由于用于选择三元组的统一负采样策略过于简单,因此 CML 需要大批量才能正常工作。由于内存限制,这使得在高维场景中难以扩展。为了缓解这个问题,我们在这里提出了一种 2 阶段负采样策略,它可以找到对学习具有高度信息量的三元组。我们的策略允许 CML 在准确性和流行度偏差方面有效工作,即使批量大小比默认统一采样所需的数量小一个数量级。我们证明了所提出的推荐策略的适用性,并在各种数据集上展示了一致的积极结果。
距离度量学习旨在表示空间中的数据点,其中邻近性解释了相似性。最近流行的人脸识别、图像检索或说话人变化检测方法将此问题形式化为三重损失优化任务,即最小化:$L=\max(D(a,p)-D(a,n)+\alpha,0)$,其中$D(a,p)$是类内(相同标签)样本(锚点和正样本)之间的距离,$D(a,n)$是类间(不同标签)样本(锚和负)之间的距离,$\alpha>0$是边际常数。主要思想是强制类间对与类内对至少相差$\alpha$,这有利于同一类样本的聚类。但是最小化 L 并不容易,因为可能的三元组的数量随着身份的数量呈三次增长。
此外,一个朴素的统一采样策略会选择 L 的梯度可以忽略不计的平凡三元组。 因此,学习可能会很慢并陷入局部最小值。为了解决这个问题,一些工作提出只选择硬样本$(D(a,p)>D(a,n))$进行训练。然而,硬样本挖掘选择具有噪声(高方差)L 梯度的三元组。然后模型可能难以有效地将类间对分开,并最终处于折叠状态。
一个宽松的替代方案是只挖掘半硬样本:三元组,其中负数不一定比正数更接近锚点,但仍会产生严格的正损失。 该策略通过避免训练集中的过拟合异常值来提高训练的鲁棒性。 它通常在第一次迭代中很快收敛,但最终会用完信息样本并停止取得进展。
可以将这种现象归因于半硬样本的 L 梯度方差集中在一个小区域。 为了解决这个问题,他们建议根据它们到锚点的距离来选择负样本。可以证明这种策略导致 L 梯度的方差在更大的范围内传播,从而始终如一地产生信息丰富的三元组。
其处理大规模目录和数据稀疏性的能力使得三重损失模型适用于推荐任务。它确实最近被提出作为 CML 模型,与传统的矩阵分解 (MF) 方法取得了有竞争力的结果。 CML 假设用户和物品可以放置在一个联合的低维空间中。然后,根据它们的欧几里德距离测量的接近度,可以轻松地完成推荐。 CML 可以达到有竞争力的准确性,但我们在本文中表明它需要大批量才能做到这一点,因为它是简单的统一负采样策略。由于内存限制,这使得 CML 无法在高维场景中扩展,例如,在构建混合多媒体推荐系统时,该系统从交互数据和高维物品内容(如音频频谱图)中共同学习。出于这个原因,将默认的统一采样替换为 2 阶段策略,该策略找到对学习始终提供信息的三元组。这使得 CML 能够在均匀采样方面具有竞争力,即使是小批量,无论是在准确性还是流行性偏差方面。
贡献有三方面:
- 研究了批量大小对 CML 性能的影响;
- 提出了一个 2 阶段的负采样,它使小批量的 CML 高效;
- 证明了本文的采样策略在三个真实世界数据集上的适用性,对于 Top-N 推荐任务,在准确性和流行度偏差方面
1. Preliminaries
1.1 问题定义
考虑一个数据集,用户数量为$N$,物品数量为$M$,二元交互矩阵$R:M\times N$,$R_{ij}$表示表示第 i 个用户和第 j 个物品之间唯一的正面隐式反馈(例如,点击、收听、查看历史记录等)。使用$S=\lbrace(i,j)|R_{ij}=1\rbrace$表示存在隐式交互的用户-物品对的集合。考虑的任务是预测可能一起交互的物品/用户。
1.2 协同过滤学习
CML 学习用户和物品的联合度量空间来编码$S$。这个想法是学习一个度量,将 S 中的正对拉得更近,同时将负对(不在 S 中的对)相对于正对推得更远,基于以下损失:
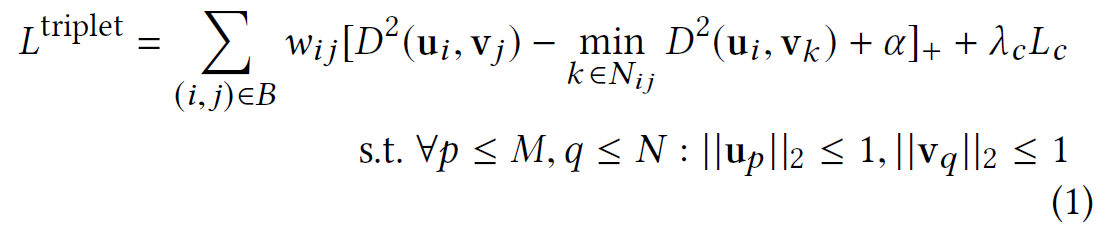
| 符号 | 表示 |
|---|---|
| $u_{i}\in R^{d}$ | 用户潜在表示 |
| $v_{i}\in R^{d}$ | 物品潜在表示 |
| $B\subset S$ | 考虑的小批量中的一组正对 |
| $N_{ij}\subset \lbrace k | (i,k)\notin S\rbrace$ |
| $\alpha>0$ | 常数边界 |
| $D$ | 欧几里得距离 |
| $w_{ij}$ | 基于$N_{ij}$中落入$\alpha$-ball 中的负数数量的权重,以惩罚较低等级的物品 |
| $[.]_{+}=\max(.,0)$ | |
| $L_{c}$ | 正则化项(由$\lambda_{c}$加权)用于去相关学习度量中的维度。 |
| $\lambda_{c}$ | 超参数 |
然后通过在潜在空间中找到她/他周围的 k 个最近的物品来为用户做出推荐。
将$w_{ij}$设置为1,用于不同采样策略之间的公平比较。此外,不会对所有模型都使用$L_{c}$,因为使用这种正则化进行均匀采样的结果较差。此外,所有用户和物品向量都归一化为单位球体:$\forall p\le M,q\le N:||u_{p}||_{2}=1$(通过在用户/物品嵌入层之后添加 L2 归一化步骤),而不是被束缚在单位球内。
2. 采样策略
2.1 Spread-out Regularization 展开正则化
为了充分利用嵌入的表达能力,潜在向量应该在空间中充分“展开”。 直观地,如果两个随机采样的非匹配向量以高概率正交,则它们是“展开”的。 为此可以证明,如果$p_{1},p_{2}$是从$R^{d}$中的单位球面独立均匀采样的两个向量,则$p_{1}^{T}p_{2}$的概率密度满足:
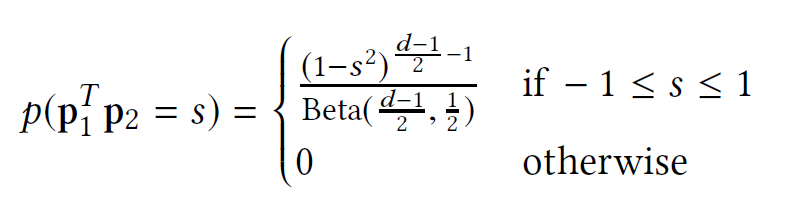
其中$Beta(a,b)$是beta分布函数。通过这个分布,可以进一步发现$E[p_{1}^{T}p_{2}]=0,E[(p_{1}^{T}p_{2})^{2}]=\frac{1}{d}$并且提出了全局正交正则化(GOR)来强制潜在向量的传播。 因此,GOR 在 CML 中的应用是:
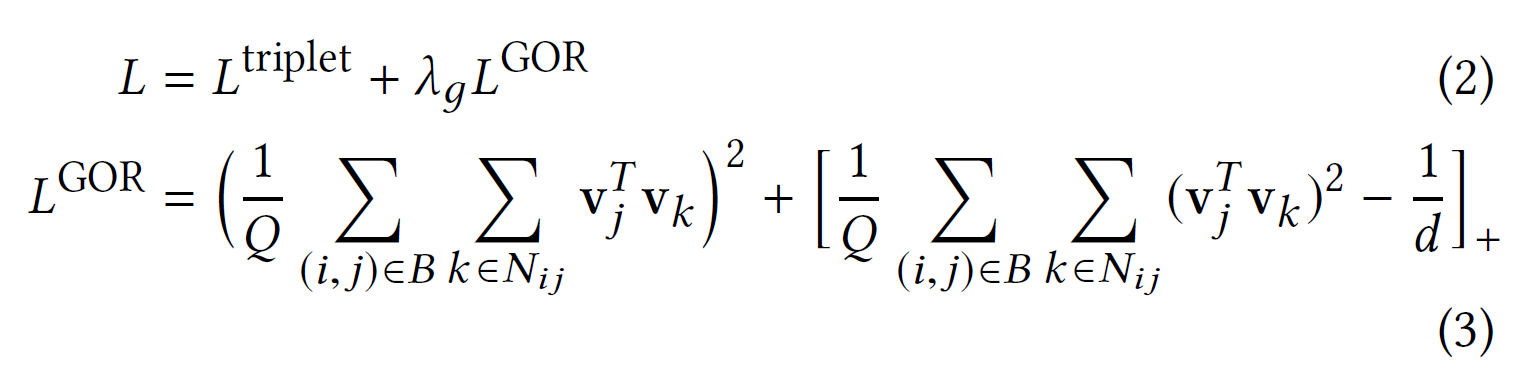
其中$\lambda_{g}$是一个超参数,$Q=|B|\times |N_{ij}|$,$d$是潜在空间的维度。
2.2 2-stage negative sampling
为了构建一个批次,首先在 S 中随机采样对,以获得锚用户和正项。策略旨在通过如下所述的 2 阶段设置替换三元组中集合$N_{ij}$负项的统一采样。
在第一阶段,根据自然语言处理中流行的 Word2Vec 算法及其在推荐任务中的应用中提出的频率,从数据集中的所有物品中采样 C 个否定候选:
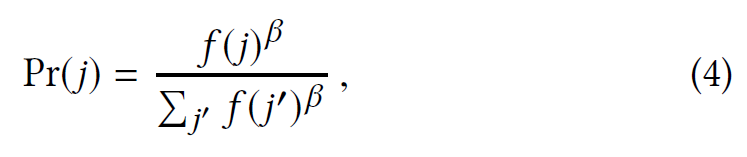
其中$f(j)$是物品$j$的交互频率,参数$\beta$起到锐化或平滑分布的作用。$\beta>0$导致采样偏爱流行物品,$\beta=0$导致物品被均匀采样,而$\beta<0$则更可能采样不受欢迎的物品。
在这项工作中,使用正样本来支持流行物品作为负样本。动机是由于交互数据中的流行偏差,流行的物品往往靠得很近。 因此,一个挑战是将不匹配的流行物品在潜在空间中推得更远。 将流行的物品分开可以帮助减少推荐中经常出现的流行偏见。
在第二阶段,从 C 个先前候选中选择信息性否定项。 给定正项$v_{j}$的潜在向量,对负项索引$n$进行采样,对应的潜在因子$v_{n}$如下:
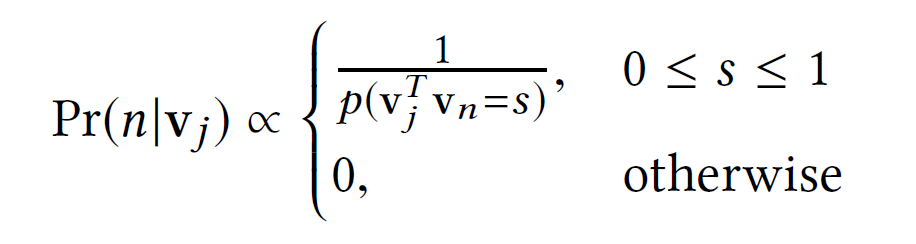
该策略有两个目标:首先,与半硬三元组采样相比,此概率函数的选择提供了梯度方差范围更大的三元组。其次,它对为 $v_{j}^{T}v_{n}$产生高正值的物品$n$赋予很高的概率,从而导致$L^{triplet}$的正值和$L^{GOR}$的大值。
当$v_{j}^{T}v_{n}>0$时,$L^{ROG}$随着$v_{j}^{T}v_{n}$的增大而增大。同时,对于每个正负对$(v_{j},v_{n})$,有$||v_{j}-v_{n}||{2}^{2}=||v{j}||{2}^{2}+||v{n}||{2}^{2}-2v{j}^{T}v_{n}=2-2v_{j}^{T}v_{n}$,所以$v_{j}^{T}v_{n}$越大,正负点越接近。这导致$D^{2}(u_{i},v_{j}),D^{2}(u_{i},v_{n})$之间的差异较小,让$L^{triplet}$更可能是正的。因此,与均匀采样情况相比,它会导致更高的损失值,并有望产生更适合训练的梯度。