本文提出用于协同过滤的双曲GCN 模型,模型可以通过边际排名损失有效地学习,并表明双曲空间在边界排序设置下具有理想的属性,称为双曲协同过滤 (HGCF)。
HGCF 通过 GCN 模块在参考点的切线空间上聚合邻域信息,从而学习双曲空间中的用户和物品表示,使用基于黎曼梯度下降优化的双曲距离的边界排序损失来有效学习。
问题描述
考虑标准隐式协同过滤设置:$m$个用户$U=\lbrace u_{1},…,u_{m}\rbrace$和$n$个物品$I=\lbrace i_{1},…,i_{n}\rbrace$。用户和物品之间的交互在一个稀疏的$m\times n$二元交互矩阵$R$中给出,其中当用户$u$和物品$i$有交互时,$R_{ui}=1$,否则$R_{ui}=0$。
定义$N_{u}=\lbrace i\in I:R_{ui}=1\rbrace$为用户邻域,表示与用户$u$有交互的项目集;类似可以定义$N_{i}=\lbrace u\in U:R_{ui}=1\rbrace$为物品邻域。
模型总述
图1总结了 HGCF 架构,为了应用 HGCF,首先为双曲空间中的所有用户和物品初始化嵌入。然后,给定具有相应嵌入$\theta_{u}\in H^{d}$的用户$u$,我们将$\theta_{u}$映射到参考点的切线空间,在切线空间中通过多层图卷积。更新后带有编码邻域信息的嵌入,被映射回$H^{d}$,在双曲空间中应用双曲边界排序损失。损失中的信号被反向传播以更新相关参数并重复该过程。类似的过程应用于项目嵌入。
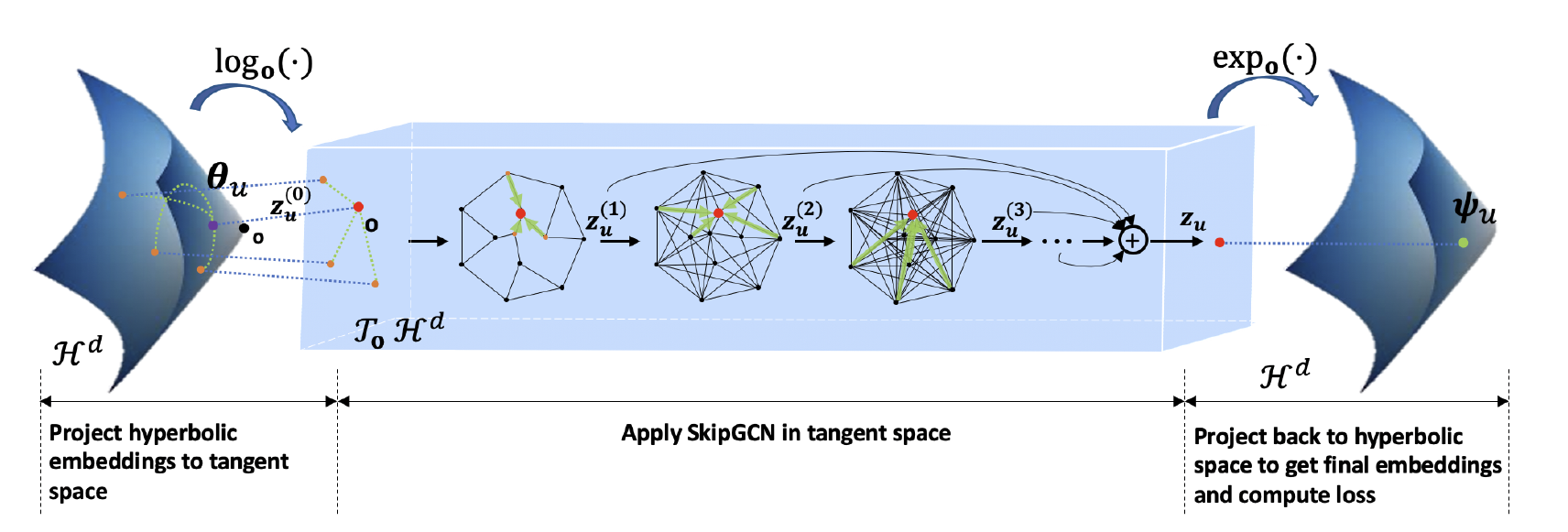
双曲嵌入
HGCF对用户和项目嵌入都使用洛伦兹表示。固定原点为$o=(\sqrt{k},0,…,0)\in H^{d}$并作为参考点。请注意,$k=-1/c$是曲率$c$的倒数,此处被视为超参数并根据经验设置。
嵌入是通过从参考点$o$的切线空间上的高斯分布采样来初始化的。形式上,给定用户$u$和项目$i$,首先从多元高斯中采样: $$ \theta_{u}',\theta_{i}'\sim N(0,\sigma I_{d\times d}) $$ 然后设置 $$ \theta_{u}''=[0;\theta_{u}']\quad \theta_{i}''=[0;\theta_{i}'] $$ 其中满足$<\theta_{u}'',o>{L}=0,<\theta{i}'',o>{L}=0$,都属于正切空间$T{o}H^{d}$。为了在$H^{d}$中获得相应的嵌入,通过指数映射投影到双曲空间$\exp_{o}:T_{o}H^{d}\to H^{d}$:
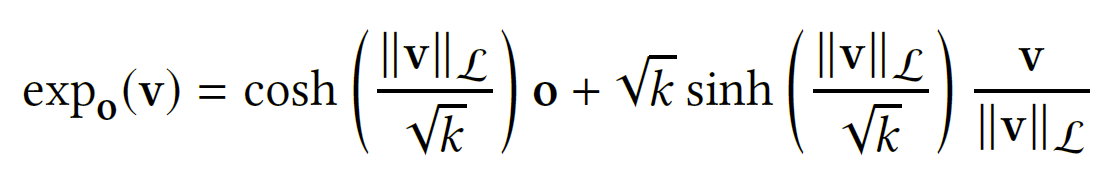
之后便可以得到用户和物品在双曲空间中的嵌入:

以上的双曲嵌入用于为所有用户和物品初始化模型。
Skip-connected 图卷积网络
GCN的主要思想是通过迭代聚合来自多跳邻居的本地信息来学习图中的节点表示。聚合过程通常涉及每个阶段的特征转换和非线性激活。然而最近的工作发现,与更简单的均值聚合方法相比,特征变换和非线性带来的收益是最小的。 此外,非线性为模型增加了相当大的表示能力,并可能导致对高度稀疏的CF数据集的导致过度拟合。 鉴于这些发现,HGCF选择去除特征变换和非线性,以降低模型复杂性并加快训练和推理速度。
HGCF在正切空间执行聚合操作,首先将嵌入通过对数映射投影到正切空间:
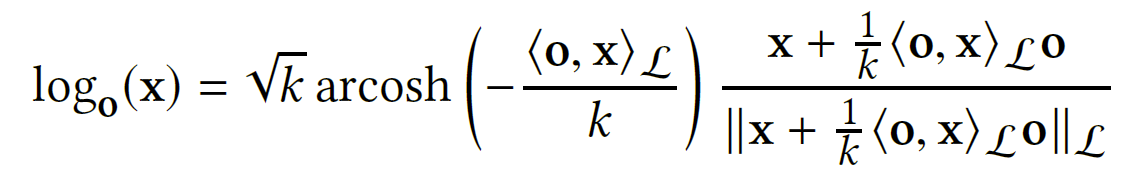
输出向量作为第一个 GCN 层的输入,分别表示为:

给定用户邻域和物品邻域,每一层图卷积层都是通过聚合来自前一层的邻域表示来计算的:
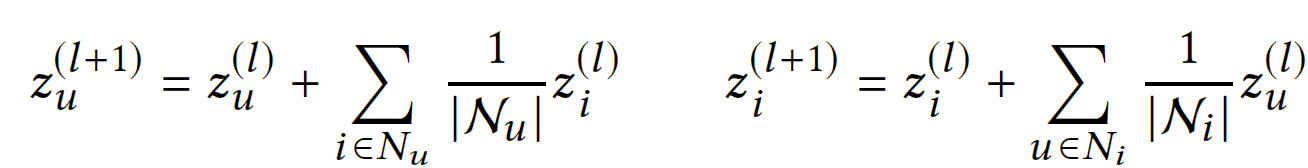
每一层都聚集在越来越高阶的邻居上,允许对用户和物品之间的长期关系进行明确建模。
为了充分利用高阶关系,需要将多个图卷积层堆叠在一起。为了减轻深度的限制,本文探索了包含由残差网络和深度 GCN 相关工作激发的跳跃连接(Skip-connected)的架构,如图2所示。
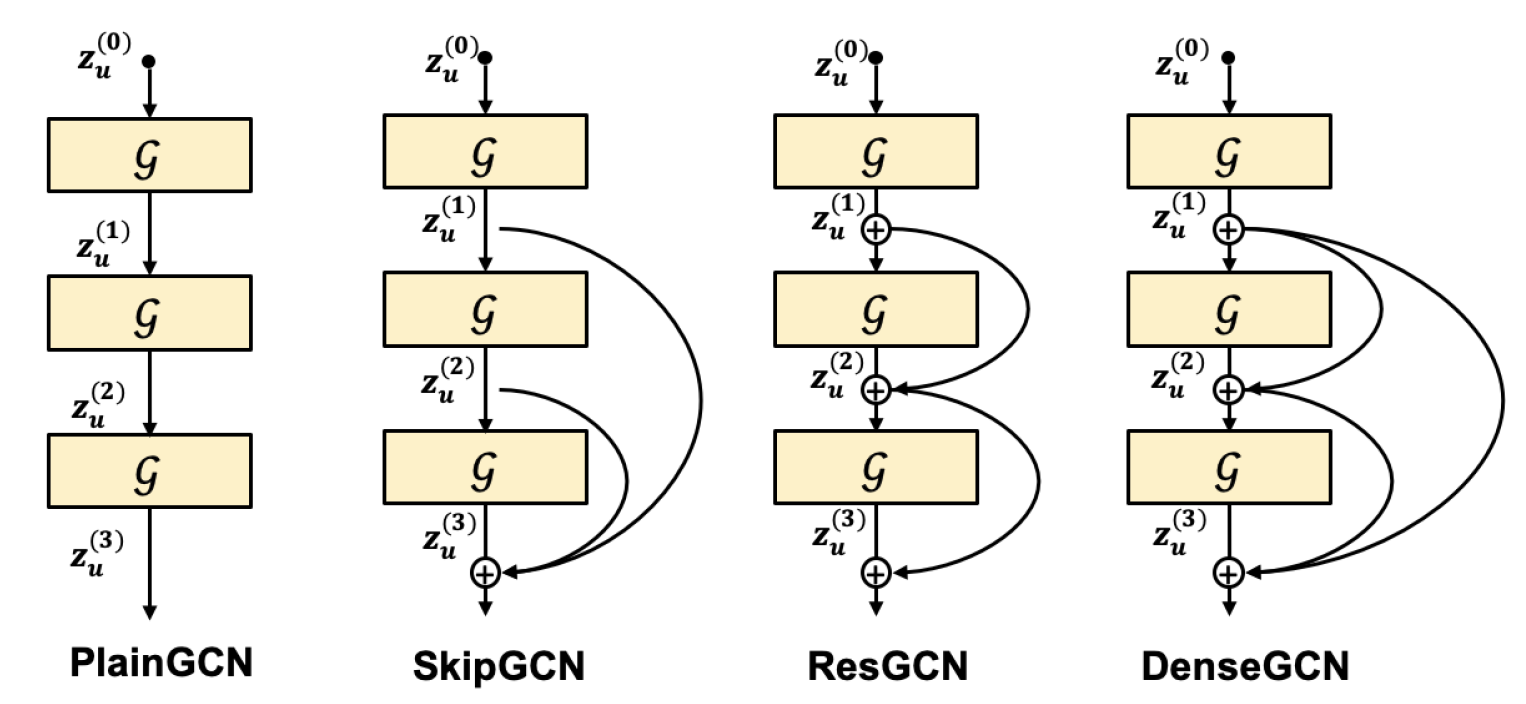
这里,PlainGCN 是原始模型,SkipGCN、ResGCN 和 DenseGCN 具有不同的跳过连接结构。 SkipGCN 包含从每一层到最后一层的跳过连接,ResGCN 具有连续层之间的残差连接,而 DenseGCN 结合了 SkipGCN 和 ResGCN。 根据经验,SkipGCN 在双曲空间设置中表现最好,将这种架构用于 HGCF。
在 SkipGCN 下,最后一层聚合来自所有中间层的表示,每个用户和项目的最终嵌入是通过应用指数映射将 SkipGCN 的输出投影回双曲空间来获得:
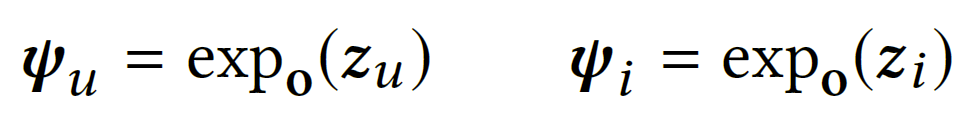
更新后的嵌入现在编码了丰富的邻域信息,可以通过双曲距离$d_{L}(\Psi_{u},\Psi_{i})$来估计用户-物品对之间的相似性。
Hyperbolic Margin Ranking Loss 双曲边界排序损失
边界排序损失已被证明对基于距离的推荐模型非常有效,这种损失旨在将正负用户-物品对分离到给定的边界。一旦达到边界,这些用户-用品对就被认为是分离良好的,不再造成损失。 这使优化能够不断地重新关注违反边界的“困难”对。HGCF模型中采用这种损失并优化双曲空间中的边界分离。
形式上,对于每个用户$u$采样一个正样例物品$i,R_{ui}=1$和一个负样例物品$j,R_{uj}=0$,目标是通过两个物品$i,j$到用户$u$的距离来分离这两个物品:
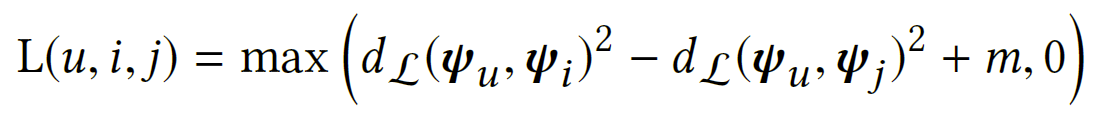
其中,$m$即为边界。一旦差异$d_{L}(\Psi_{u},\Psi_{i})^{2}-d_{L}(\Psi_{u},\Psi_{j})^{2}$大于边际,损失就变为0,物品对停止对梯度做出贡献。