Session-aware Linear Item-Item Models for Session-based Recommendation (arxiv.org)
基于会话的推荐旨在根据会话中先前消费的物品的序列预测下一个物品,例如电子商务或多媒体流服务。 具体来说,会话数据表现出一些独特的特征,即会话一致性和会话内物品的顺序依赖性、重复的物品消费和会话时效性。 本文提出了简单而有效的线性模型来考虑会话的整体方面。具体来说:
- 综合考虑了基于会话的推荐的各个方面;
- 实现了可扩展性。
首先,设计了两个专注于会话不同属性的线性模型:
- Session-aware Linear Item Similarity (SLIS) 模型旨在更好地处理会话一致性;
- Session-aware Linear Item Transition (SLIT) 模型更关注顺序依赖。
对于 SLIS 和 SLIT,放宽合并重复项的约束,并引入了权重方案以考虑会话的及时性。 结合这两种类型的模型,提出了一个统一的模型,即会话感知物品相似性/转换(SLIST)模型,这是一种全面覆盖会话各种属性的通用解决方案。
1. 基本定义
1.1 Linear item-item models
给定两个矩阵$X$和$Y$,线性模型是用一个物品到物品的相似度矩阵$B\in R^{n\times n}$来制定的:

$B$将$X$中之前消费过的物品映射到$Y$中接下来观察到的物品中。该线性模型的典型目标函数是通过最小化普通最小二乘法 (OLS) 的岭回归公式化的。
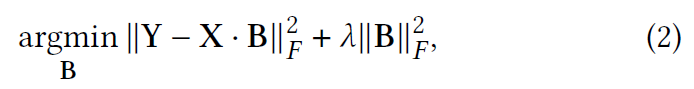
其中 𝜆 是正则项,$||\cdot||_{F}$表示 Frobenius 范数。
在传统的推荐中,每个用户被表示为所有消费物品的集合,没有会话的概念,X 和 Y 被视为相同的矩阵。SLIM 强制 B 中的所有条目都为非负且对角线元素为零。
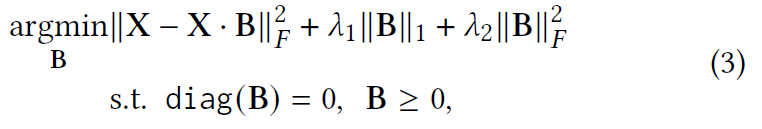
最近,$EASE^{R}$及其变体从等式(3)中删除了 B 和 L1 范数约束的非负约束,只留下对角约束。
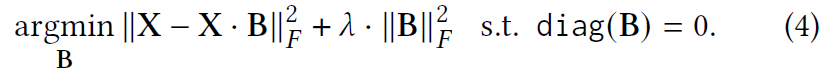
$EASE^{R}$通过拉格朗日乘子绘制闭式解:
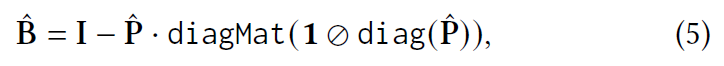
此外,diagMat(x) 表示从向量 x 展开的对角矩阵。最后,B 中的每个学习权重由下式给出
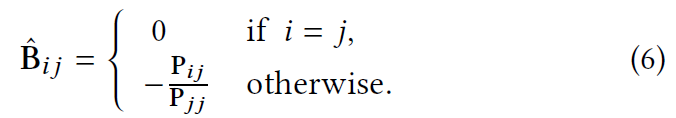
尽管反转正则化的 Gram 矩阵是大规模数据集的瓶颈,但封闭形式的表达式在效率上具有显着优势。 $EASE^{R}$的复杂度与物品的数量成正比,通常远小于现实场景中的用户数量。 它还实现了与传统推荐设置中最先进模型相比具有竞争力的预测准确性。 受这些优势的启发,我们利用线性模型的优势进行基于会话的推荐。
2. 论文模型
2.1 动机
首先展示会话的有用特征。 前三个是关于会话中物品之间的相关性,即会话内属性,而最后一个是关于会话之间的关系,即会话间属性。
-
Session consistency 会话连续性
会话中的物品列表通常在主题上是连贯的,反映了特定且一致的用户意图。 例如,用户生成的播放列表中的歌曲通常有一个主题,例如相似的情绪、相同的流派或艺术家。
-
Sequential dependency 顺序依赖
有些物品往往以特定的顺序被观察到。 在大多数会话中,通常首先使用一个物品,接着另一个。 一个直观的例子是电视剧,它的剧集通常是按顺序观看的。 出于这个原因,当前会话中的最后一个物品通常是预测下一个物品的最有用的信号。
-
Repeated item consumption 重复物品消费
用户可能会在单个会话中多次重复消费一个物品。 例如,用户可能会反复收听她最喜欢的歌曲。 此外,用户可能多次点击同一产品以将其与其他产品进行比较。
-
Timeliness of sessions 会话及时性
一个会话通常反映用户当前的兴趣,而此类会话的集合通常反映最近的趋势。 例如,许多用户倾向于更频繁地观看新发布的音乐视频。 因此,与过去的会话相比,最近的会话可能是预测用户当前兴趣的更好指标。
本文的会话感知线性模型,不仅可以同时适应会话的各种属性,而且具有高度可扩展性。
2.2 会话表示
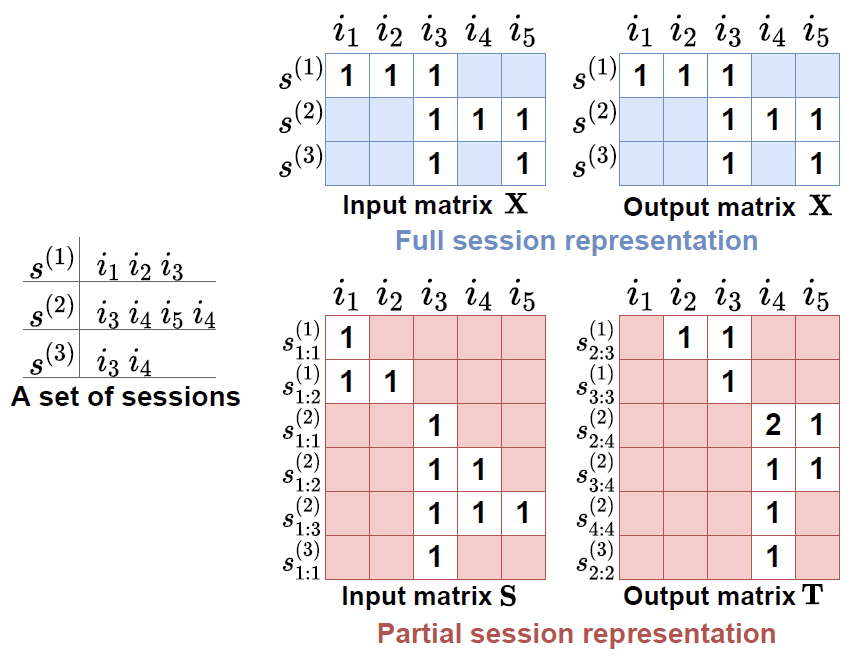
尽管会话具有顺序性质,但线性模型仅将一组物品作为向量处理。如图 2 所示,考虑两个会话表示。
-
Full session representation 完整会话表示
整个会话表示为单个向量,并且忽略会话中物品的顺序。如图 2 所示,训练示例 (𝑚) 的数量等于会话数。 它更适合会话中的物品之间往往具有更强的相关性,对消费顺序相对不敏感的情况。 请注意,会话中的重复项被视为单个项,因为完整会话表示主要处理跨项的会话一致性。
-
Partial session representation 部分会话表示
会话分为过去和未来两个子集,以表示物品之间的顺序相关性。 对于某个时间步 𝑡 ,过去的集合包含在 𝑡 之前已经消费过的物品。
2.3 会话感知的线性模型
首先,设计了两个分别利用完整和部分会话表示的线性模型。 然后,统一两个线性模型以完全捕捉会话的多方面。
2.3.1 Session-aware Linear Item Similarity Model (SLIS)
我们提出了一个使用完整会话表示的线性模型,重点是物品之间的相似性。 如第 2.2 节所述,输入和输出矩阵 (X) 相同,即$X=X\cdot B$。本文通过重新制定SLIM的目标函数来提出一个新的线性模型,以适应会话的及时性和会话中重复的物品消耗:
- 采用权重矩阵$W\in R^{m\times n}$,与$||X-X\cdot B||_{2}^{F}$相对应,假设会话的时效性随时间衰减,使用$W$来区分会话的时效性;
- 放宽$B$的零对角约束以处理重复的物品消费。 由于 B 的对角元素受到松散惩罚,模型允许重复预测与下一个物品相同的物品。
形式上,SLIS 的目标函数由下式表示:
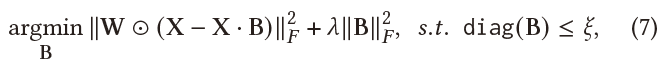
方程(7)中的目标函数是方程(4)中$EASE^{R}$目标函数的广义版本。$EASE^{R}$的主要优势在于其封闭形式的解决方案。我们仍然可以通过 Karush-Kuhn-Tucker (KKT) 条件为没有 W 的松弛对角线约束实现封闭形式的解决方案。 然而,对于任意权重矩阵 W,获得封闭形式的解并非易事。
为了解决这个问题,我们处理 W 的两个特殊情况:会话权重和物品权重。 物品的权重不影响学习B。因此,我们只考虑会话的权重;$W$被视为会话的权重向量,以区分会话的重要性。 让$w_{full}$表示 S 中每个会话的权重向量。然后,将 W 替换为会话权重和一向量的外积,即$W_{full}=w_{full}\cdot 1^{T}$,其中$w_{full}\in R^{m},1\in R^{n}$。带有$W_{full}$的线性模型由封闭式方程求解。
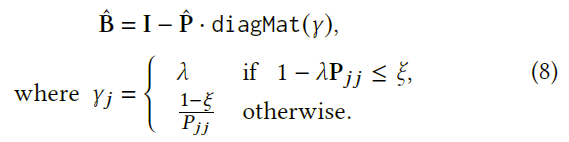
最后,我们描述了如何为 W 设置会话的权重。我们假设会话的重要性随时间衰减。 为了反映会话的及时性,我们通过以下方式为最近的会话分配更高的权重:
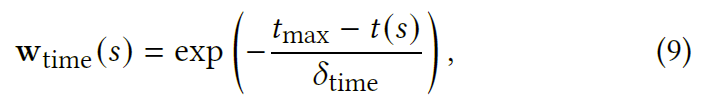
2.3.2 Session-aware Linear Item Transition Model (SLIT)
使用第 2.2 节中的部分会话表示,我们设计了一个线性模型来捕获跨物品的顺序依赖性。 与 SLIS 不同,每个会话被拆分为多个部分会话,形成不同的输入和输出矩阵。 与 SLIS 类似,我们也将会话的权重纳入 SLIT。 同时,我们忽略了 B 中对角元素的约束,因为不同的输入和输出矩阵自然不受平凡解的影响。
正式地,我们使用部分会话表示来制定 SLIT 的目标函数。
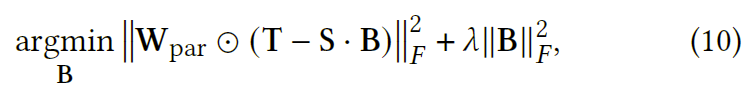
虽然 S 和 T 不同,但我们仍然推导出闭式解:
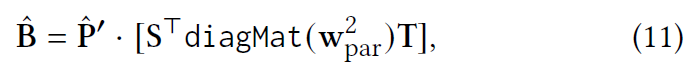
最后,我们描述了如何调整 S 和 T 中过去和未来物品子集的重要性,我们利用两个物品之间的位置差距作为物品的权重。
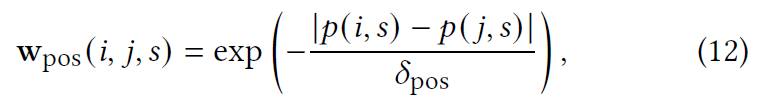
当给定一个目标物品时,可以根据顺序衰减部分会话中物品的重要性。
2.3.3 Unifying Two Linear Models
由于 SLIS 和 SLIT 捕获了会话的各种特征,我们提出了一个统一的模型,称为会话感知线性相似性/转换模型 (SLIST),通过联合优化这两个模型:
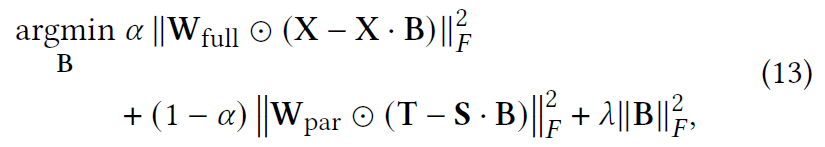
其中𝛼是控制SLIS和SLIT重要性比的超参数。
尽管乍一看似乎无法实现封闭形式的解决方案,但我们仍然可以推导出它。 直觉是,当为 SLIS 和 SLIT 堆叠两个矩阵时,例如 X 和 S,SLIST 的目标函数类似于 SLIT 的目标函数。 形式上,闭式解由下式给出:
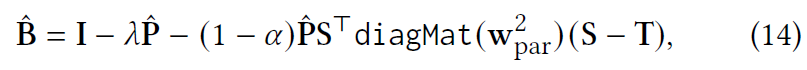
2.3.4 Model Inference
我们使用学习的物品-物品矩阵预测给定会话的下一个物品,其中包含一系列物品,即$\hat{T}=S\cdot \hat{B}$。对于推理,有必要根据 S 中的物品序列来考虑物品的重要性。与等式(12)类似,我们随着时间的推移将用于推理的物品权重衰减为
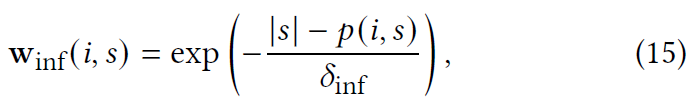
其中$\delta_{inf}$是控制推理物品权重衰减的超参数,|𝑠 | 是会话的长度𝑠。 换句话说,SLIST 将通过部分表示的向量作为输入,并将其与物品权重一起使用。